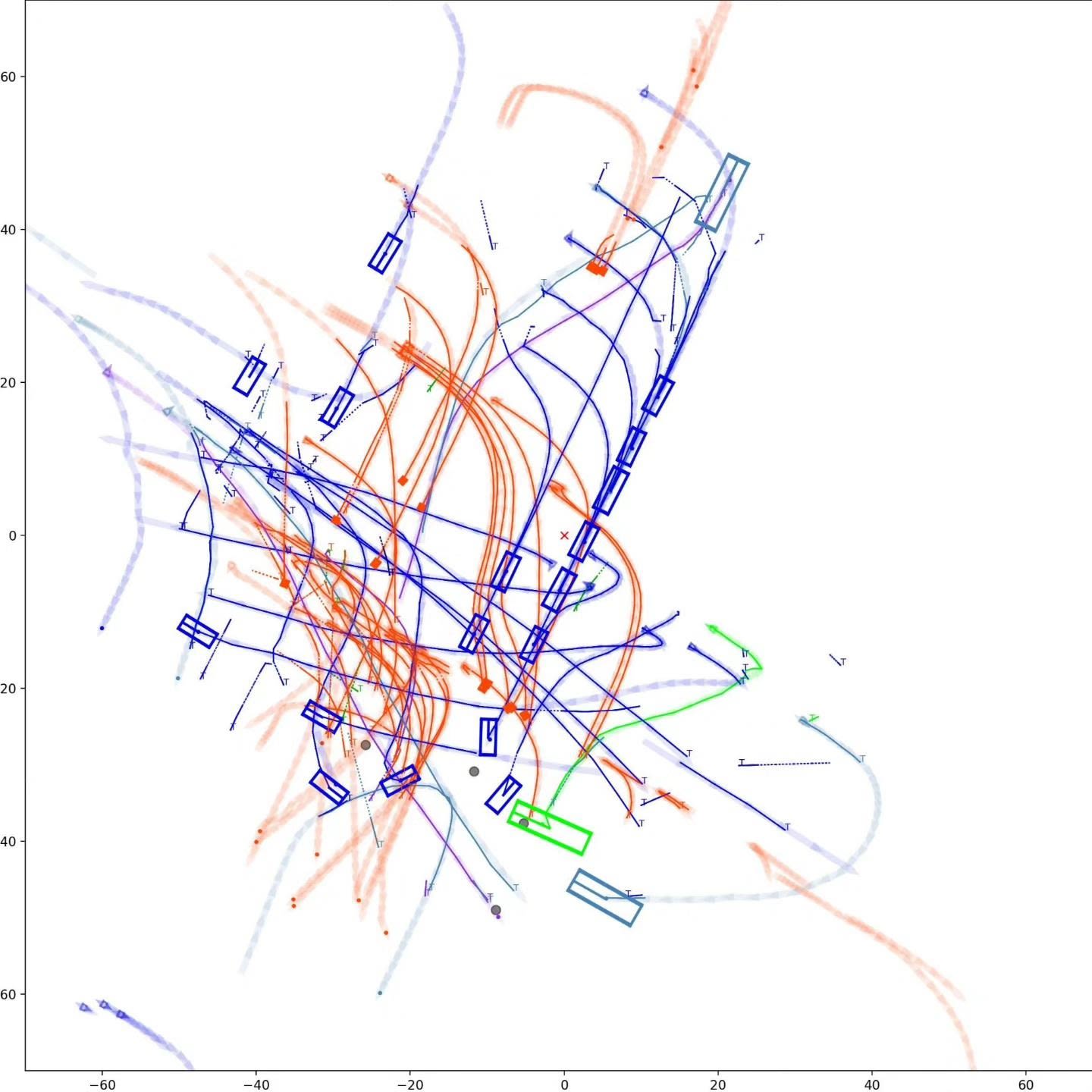
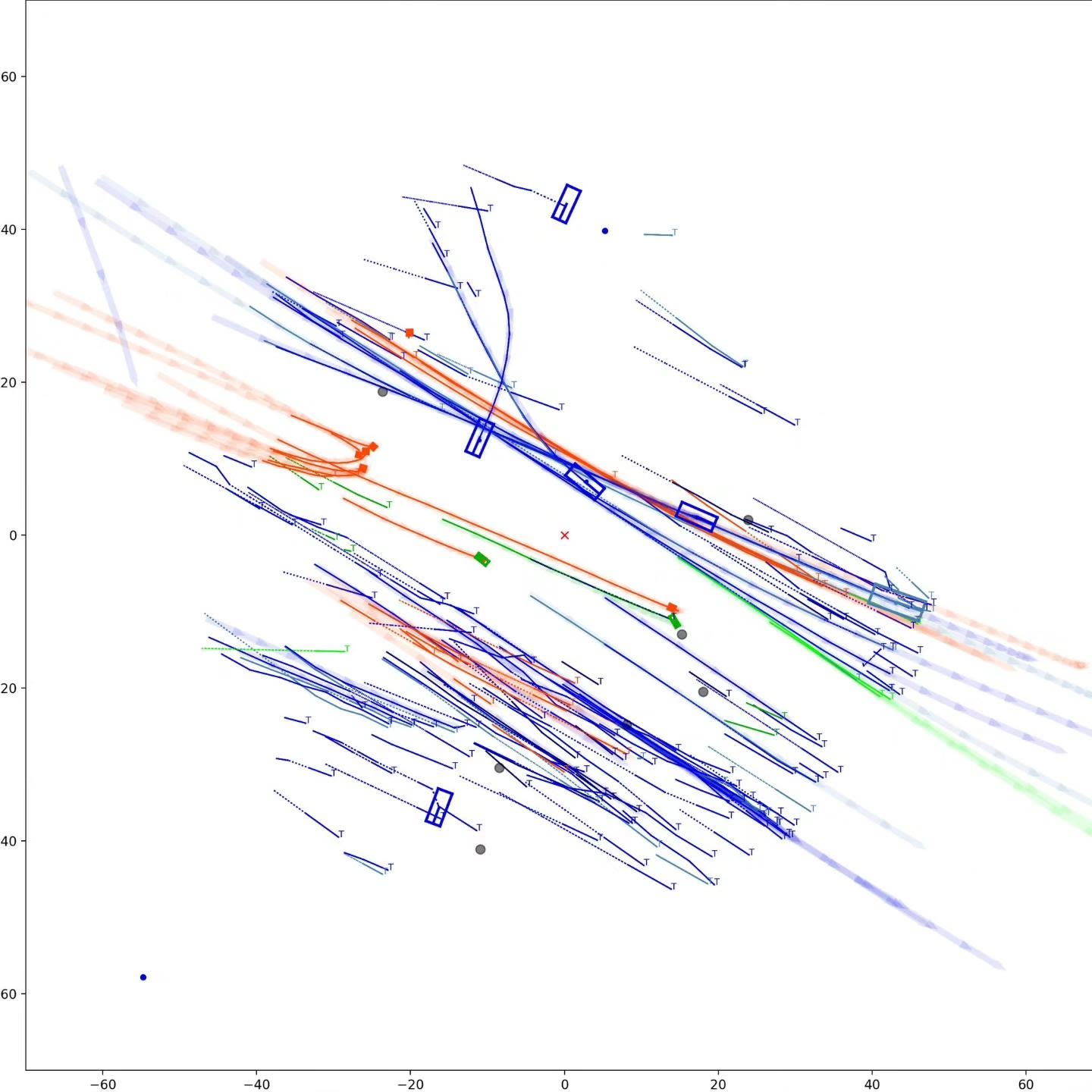
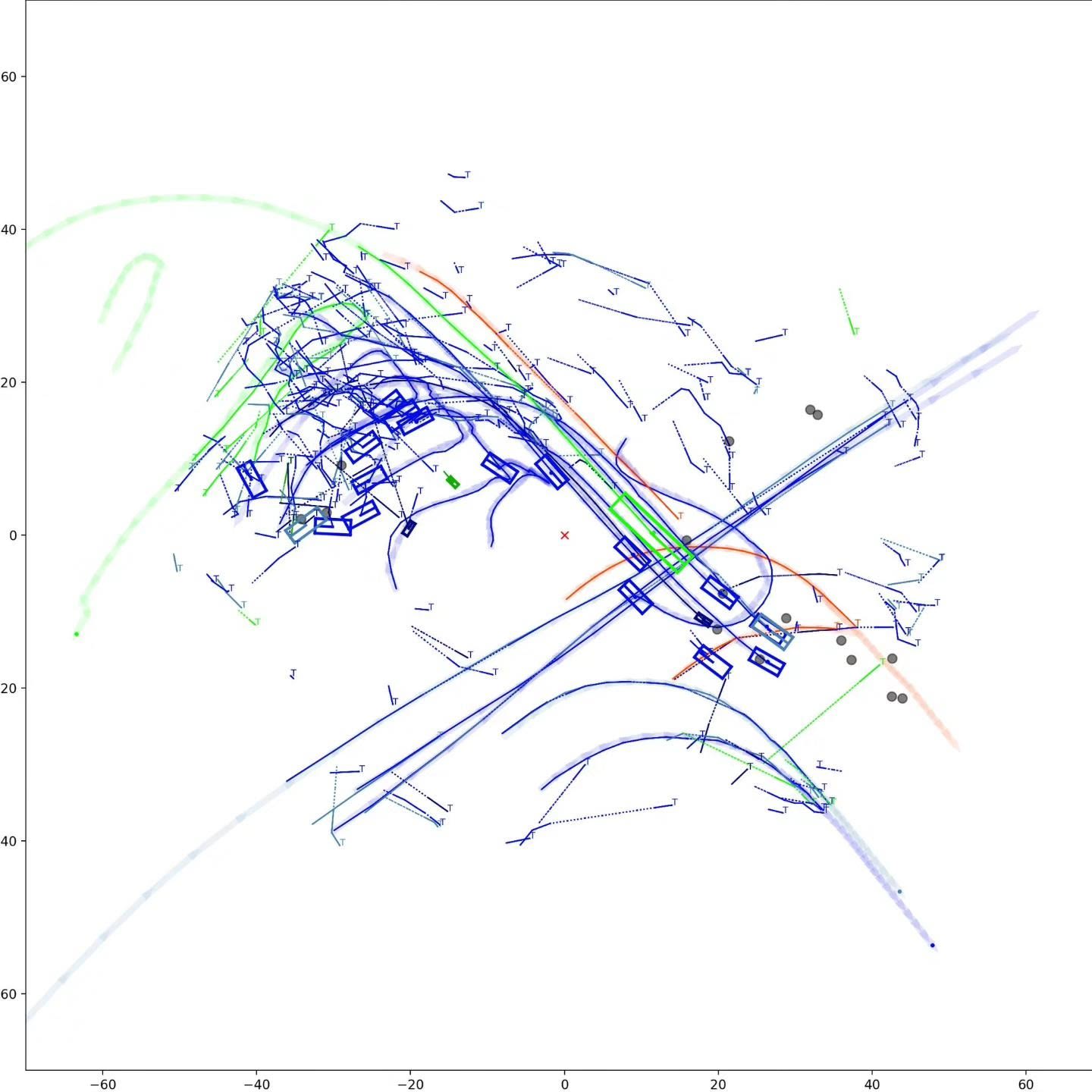
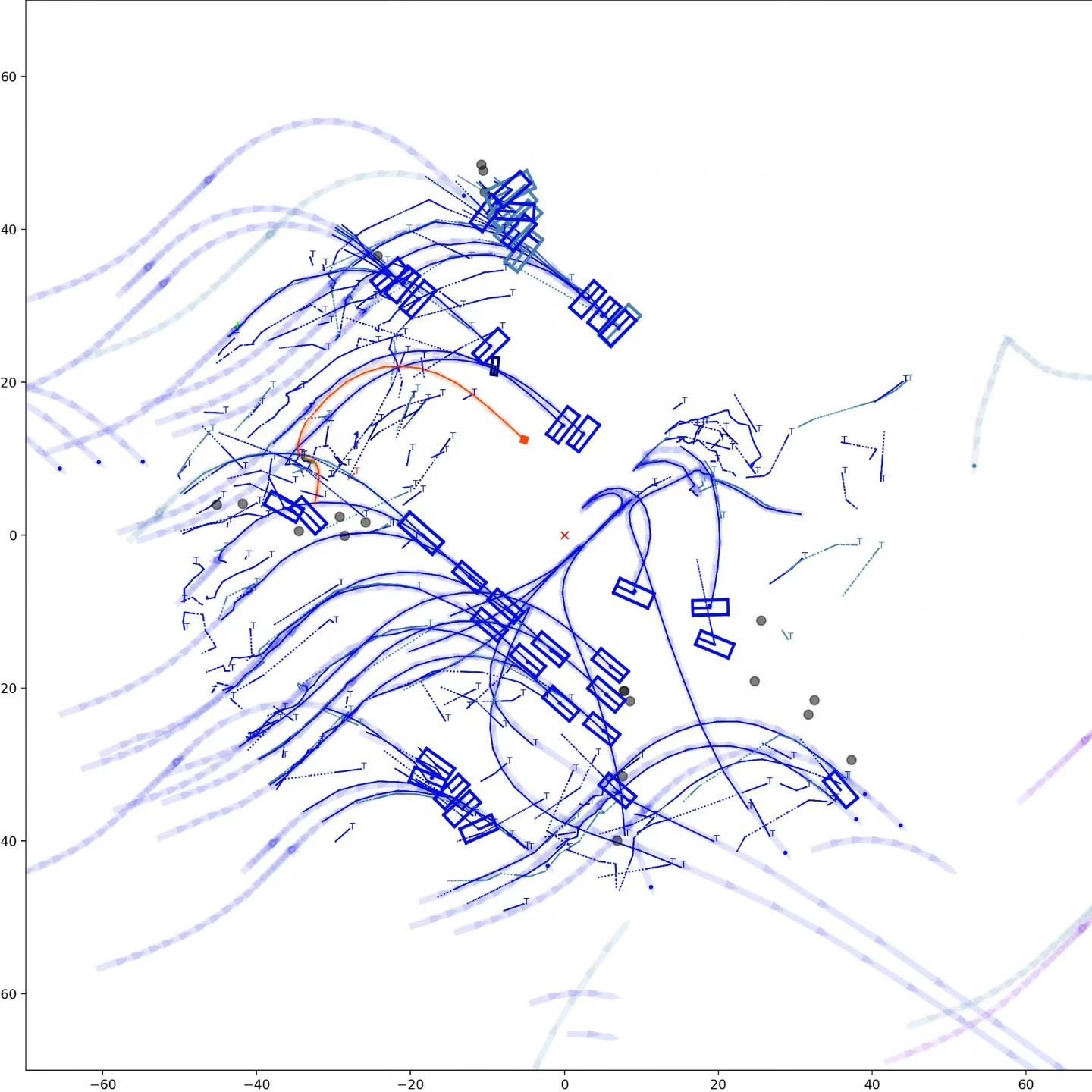
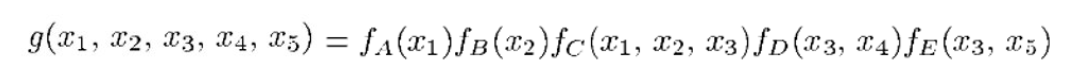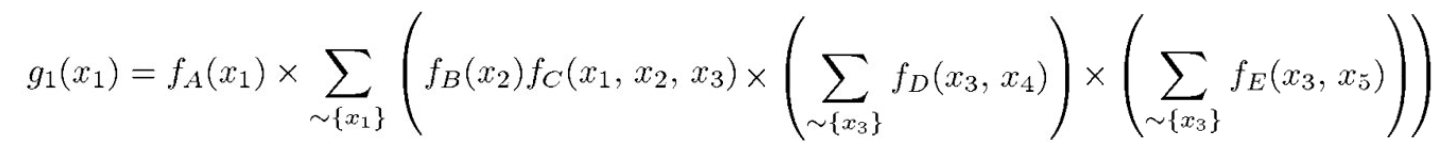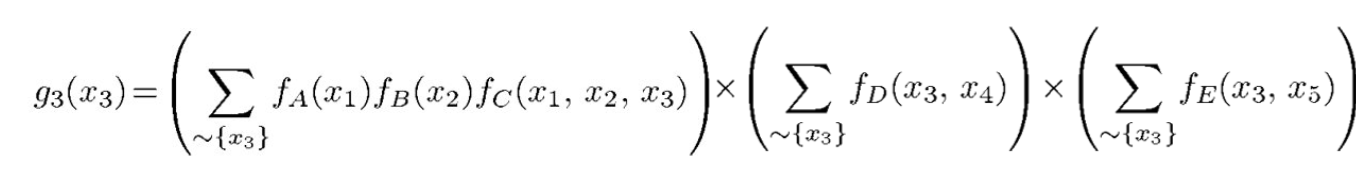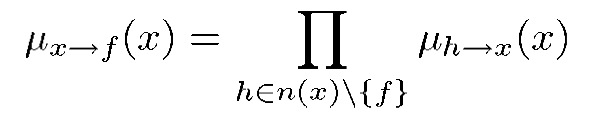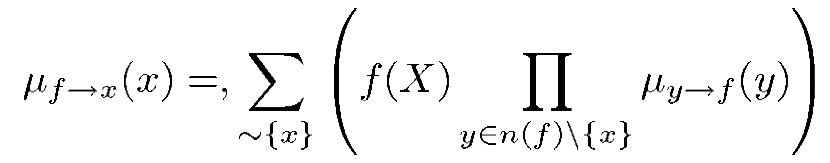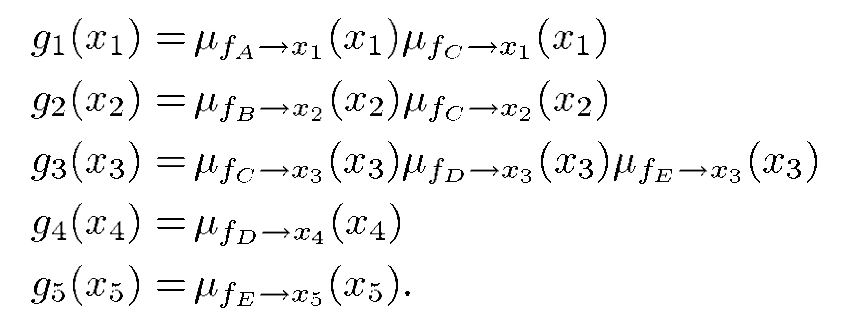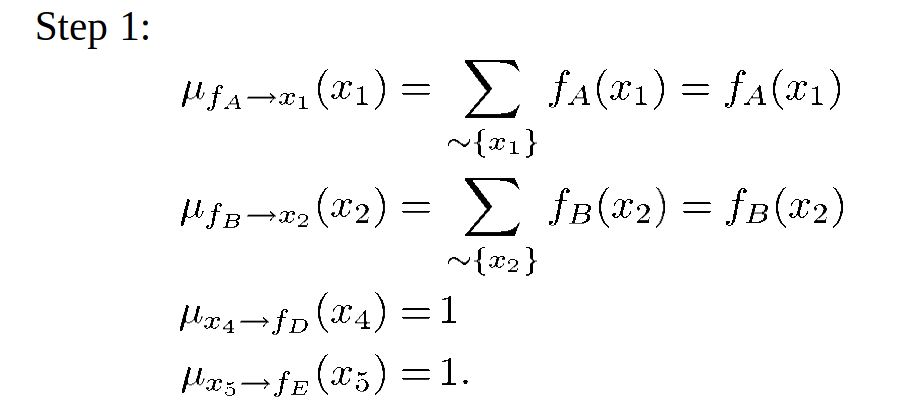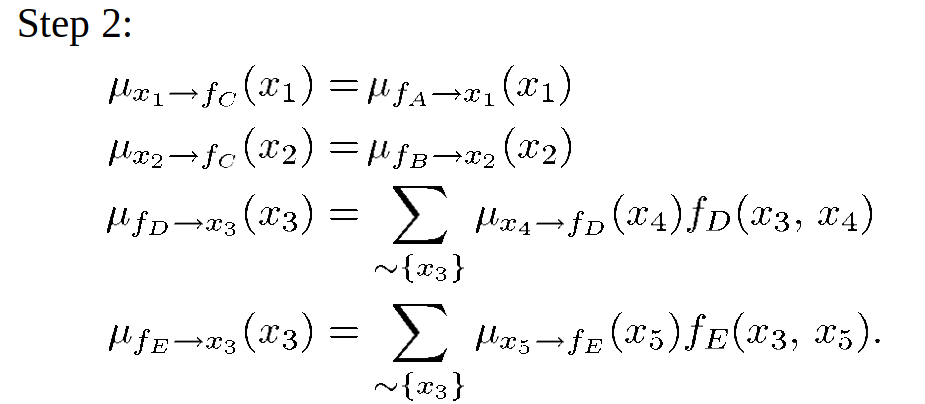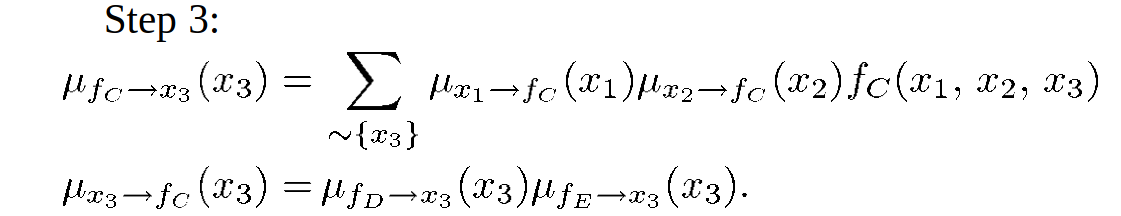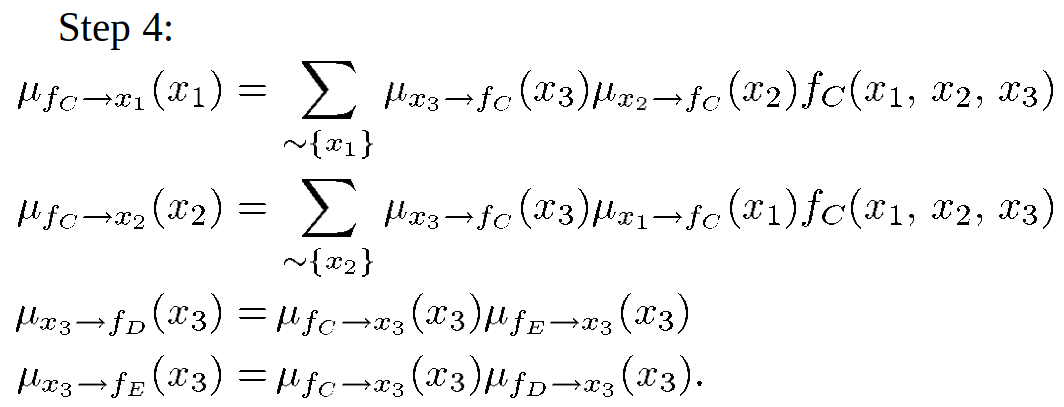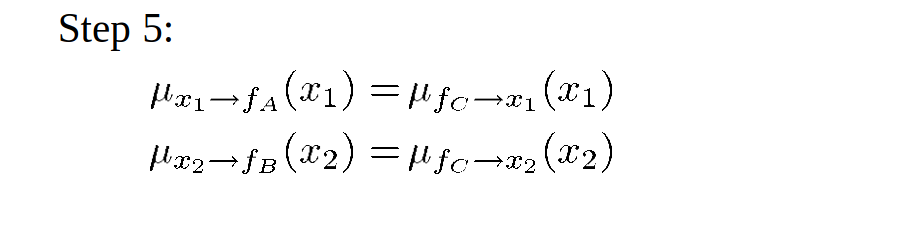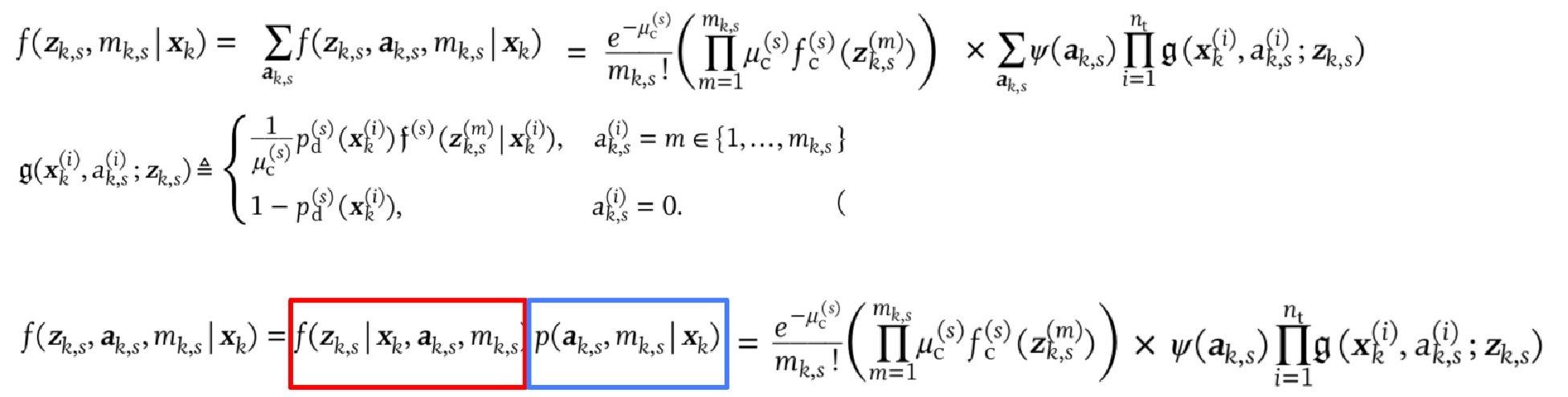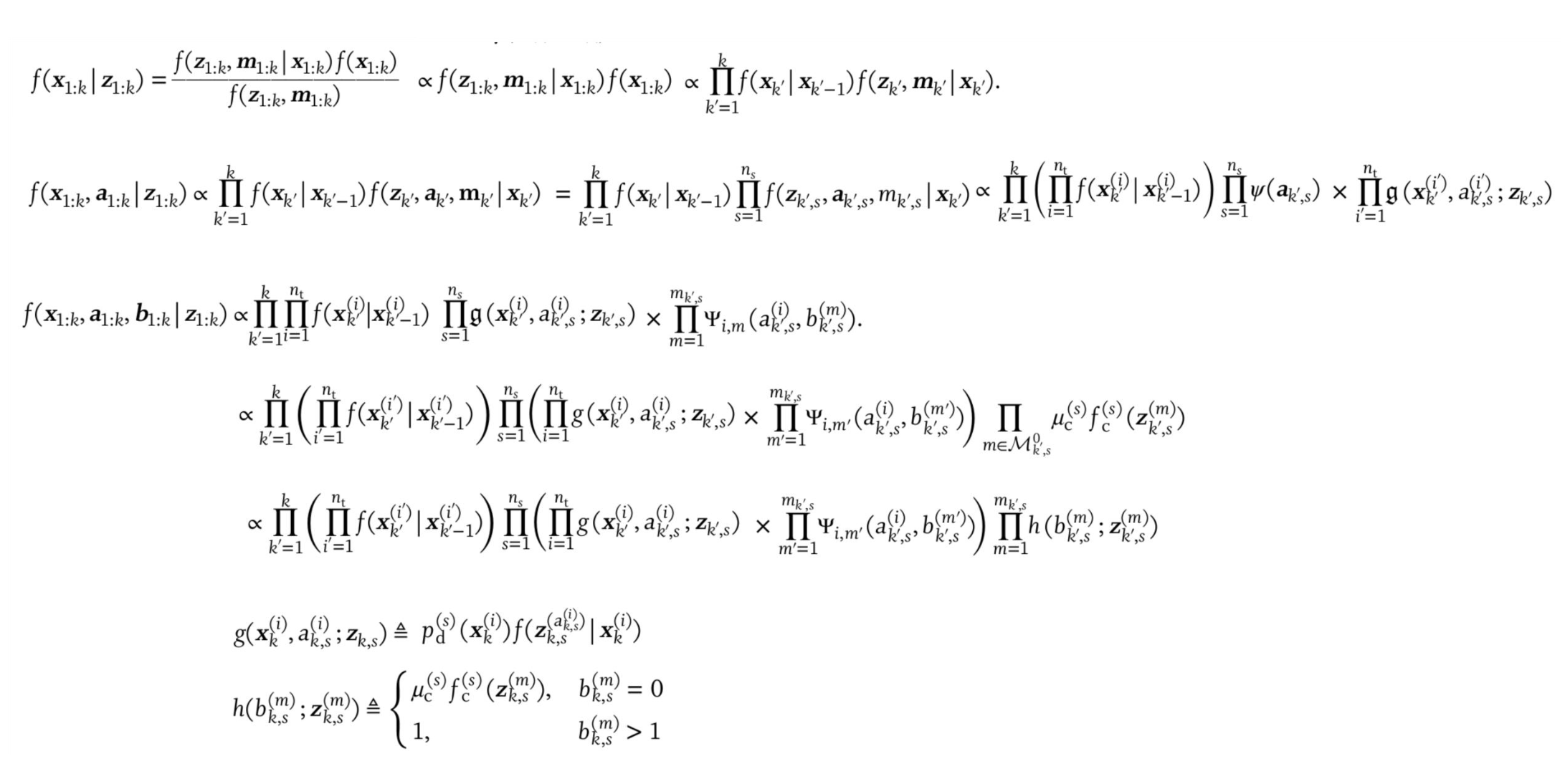Graph-based Multi-Object Tracking Results Visualization
This presentation is a summary of the previous project from a while ago. There is nothing new here, just an implementation of established methods.
Some of the previous projects were conducted under difficult circumstances, so approaching those set of material with critical eyes. Just a side note, people need to learn to see through the marketing nonsense at certain point. All those blow ups of Chinese autonomous driving companies, are we really surprised given what kind of people it attracts?
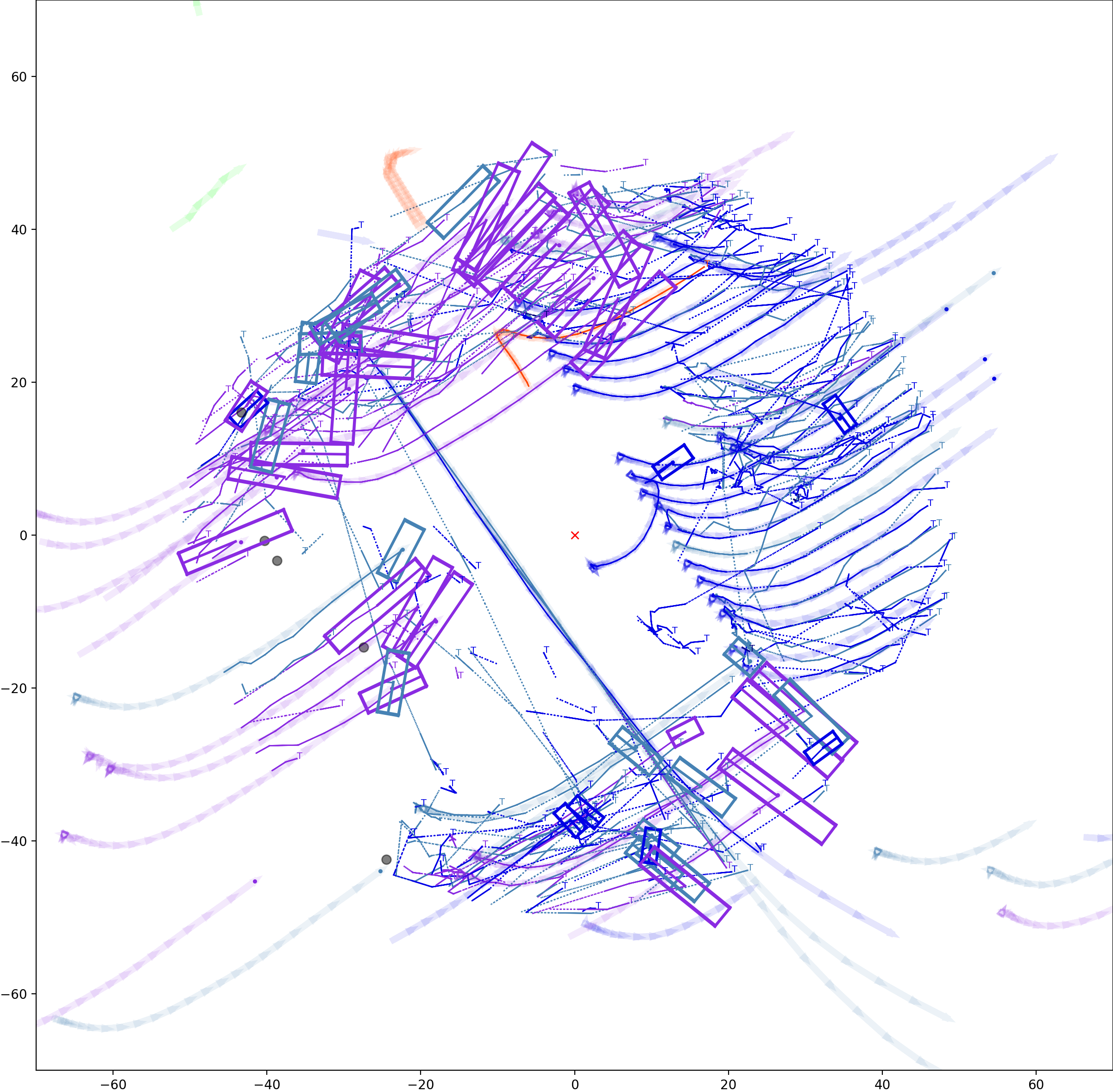
ID Assignment for Tracked Objects in Close Vicinity
Why is ID assignment, i.e., data association, so important
Accurate ID assignment is crucial. This issue compounds over time, meaning that a single erroneous association can propagate through subsequent steps.
For SLAM, association errors can be fatal at times, as introduced in this lecture
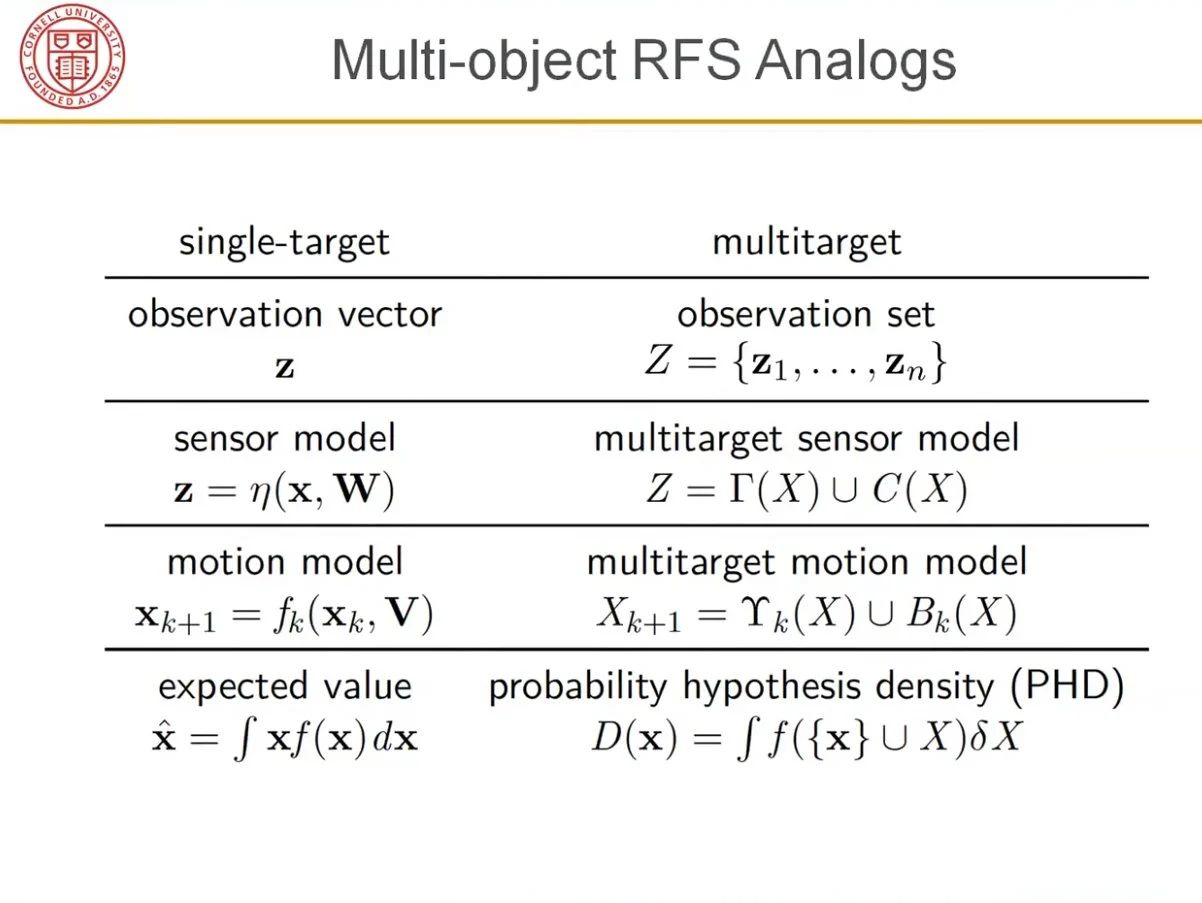
What is Multi Object Tracking
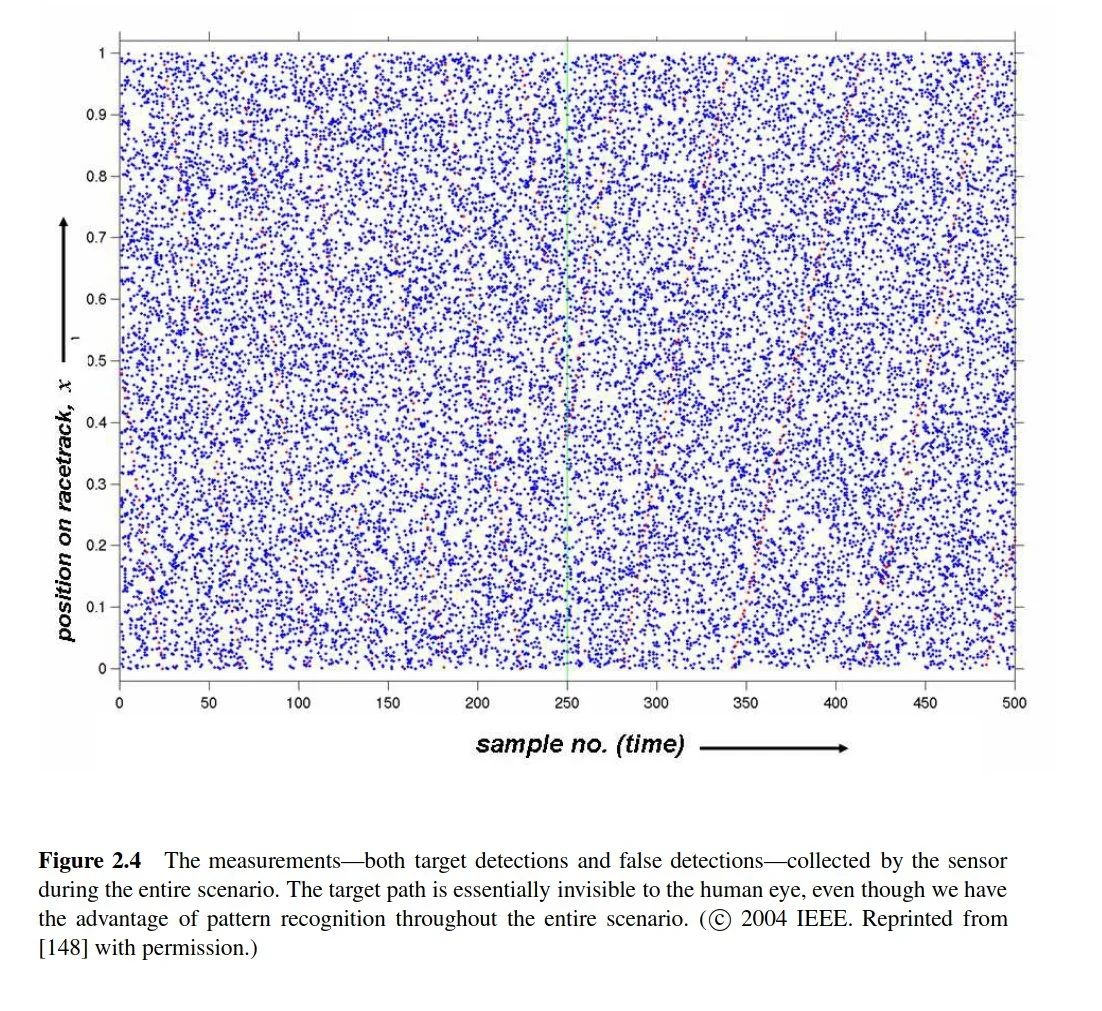
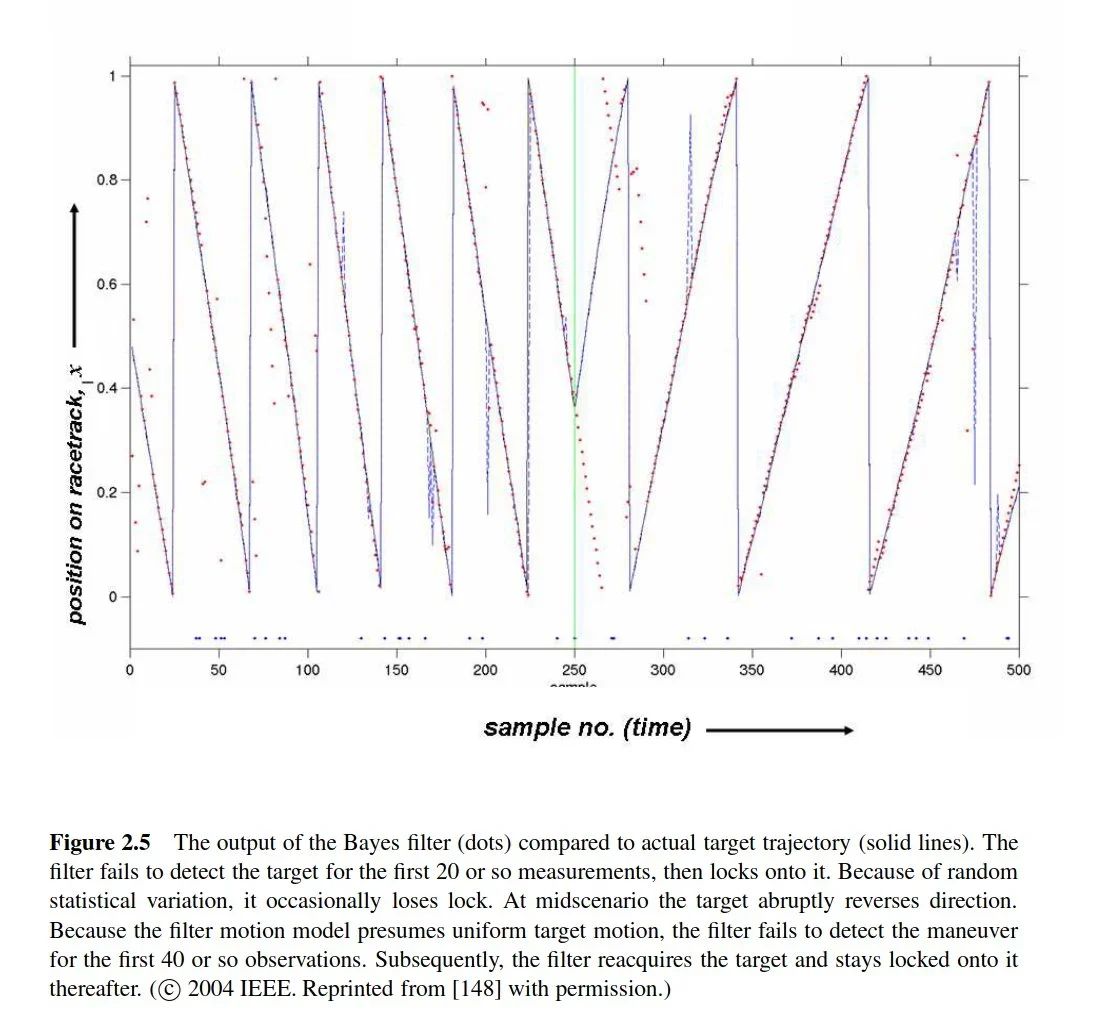
These plots are taken from Mahler's book, illustrating the complex challenge of multi-object tracking: identifying the most plausible tracks amidst false alarms and missed detection. As depicted in these plots, while there are several tracks, the detection process is significantly obscured by clutter and missed detection, the latter of which cannot be shown. Fusion aims to extract the most accurate information, in a statistical sense, from data collected by numerous imprecise sensors.
Different types of estimators, such as the least squares estimator, maximum likelihood estimator, and maximum a posteriori estimator, are discussed. Steven Kay's book provides a comprehensive theoretical background on these estimators. These estimators can yield varying tracking outcomes, especially when the objects being tracked are in close proximity to each other.
The maximum likelihood estimator is arguably the most commonly used for deterministic distributions. The maximum a posteriori estimator is frequently favored when the parameter follows a distribution.
However, a significant challenge with these estimators is that they are not always guaranteed to exist, and even when they do exist, finding them is not assured. To address these issues, more sophisticated theoretical frameworks, such as the Cramer-Rao lower bound, have been developed. Steven Kay's book methodically explores these concepts.
Simulation Result
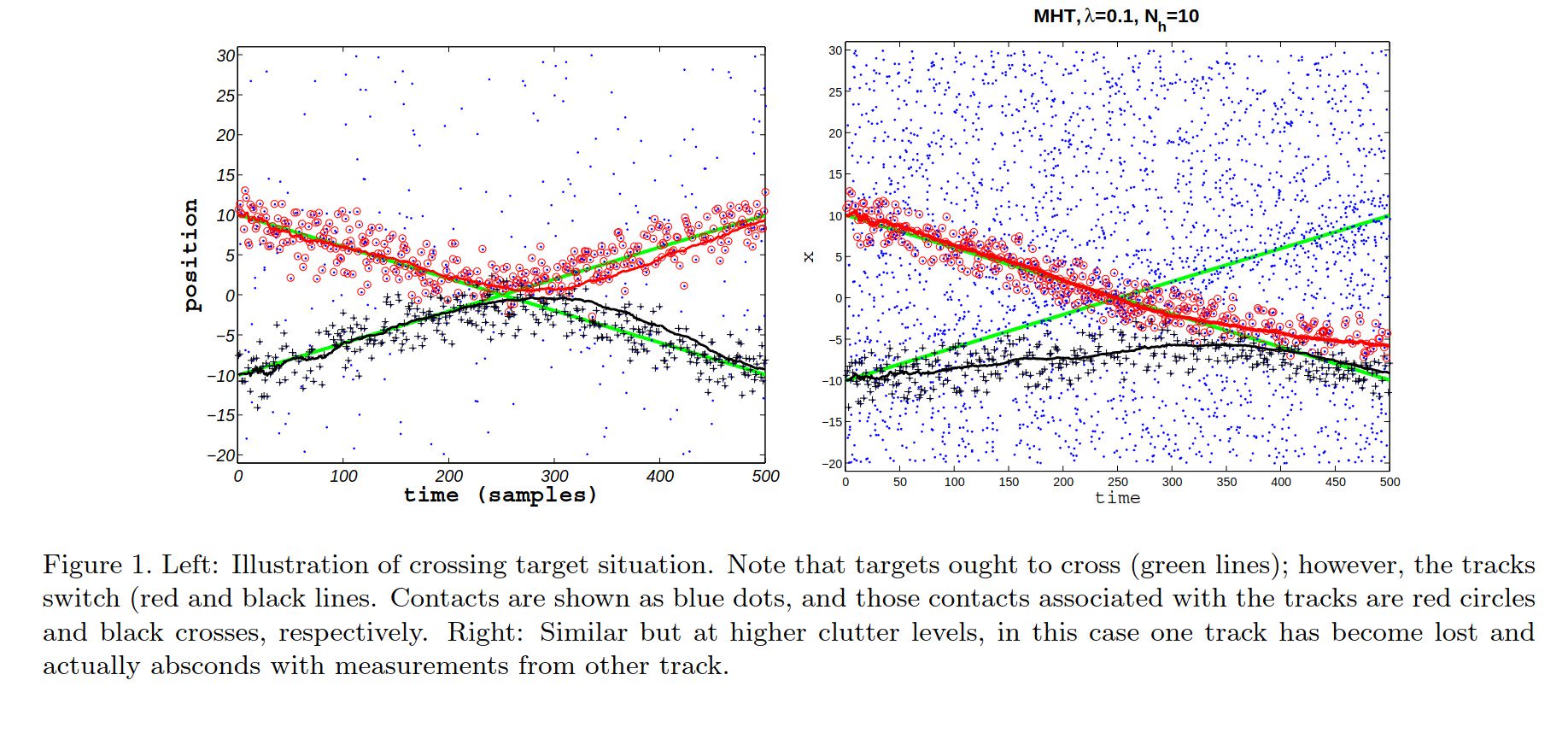
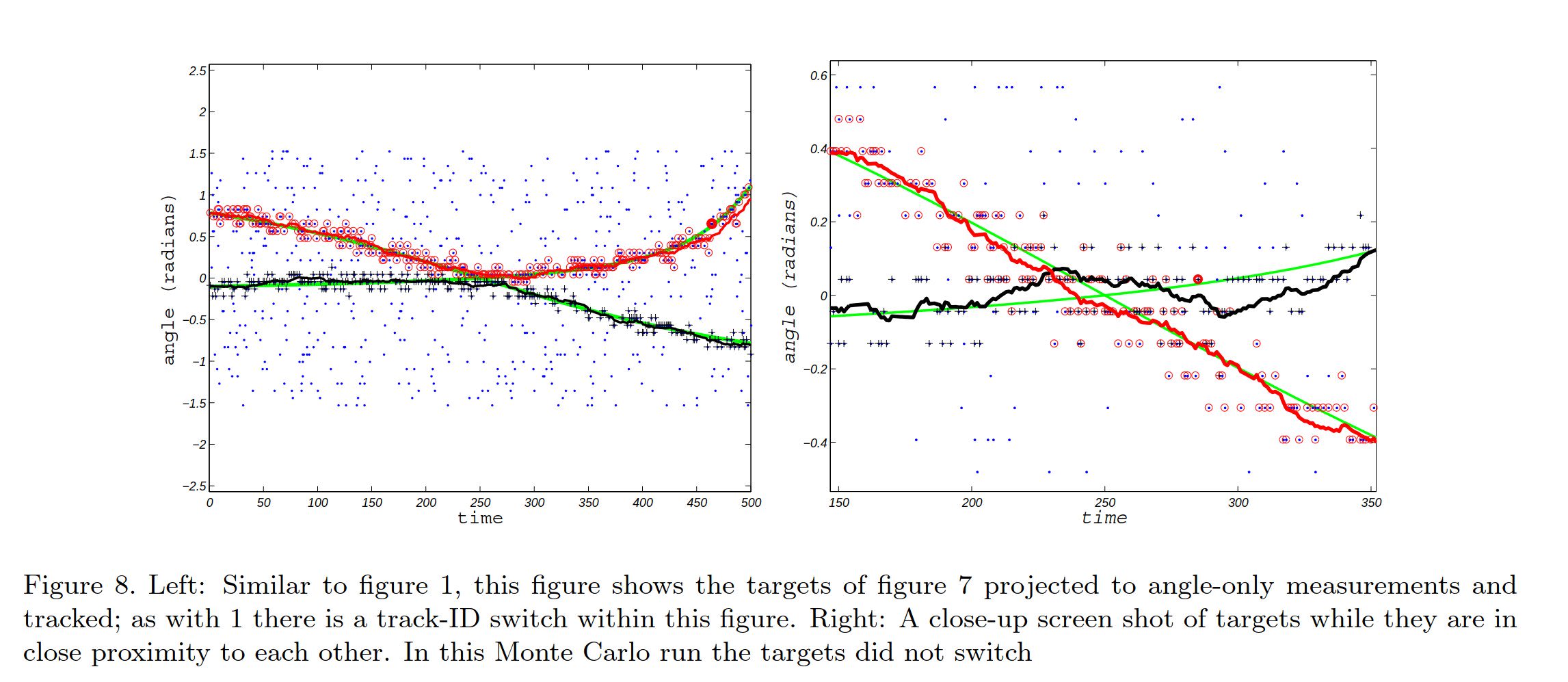
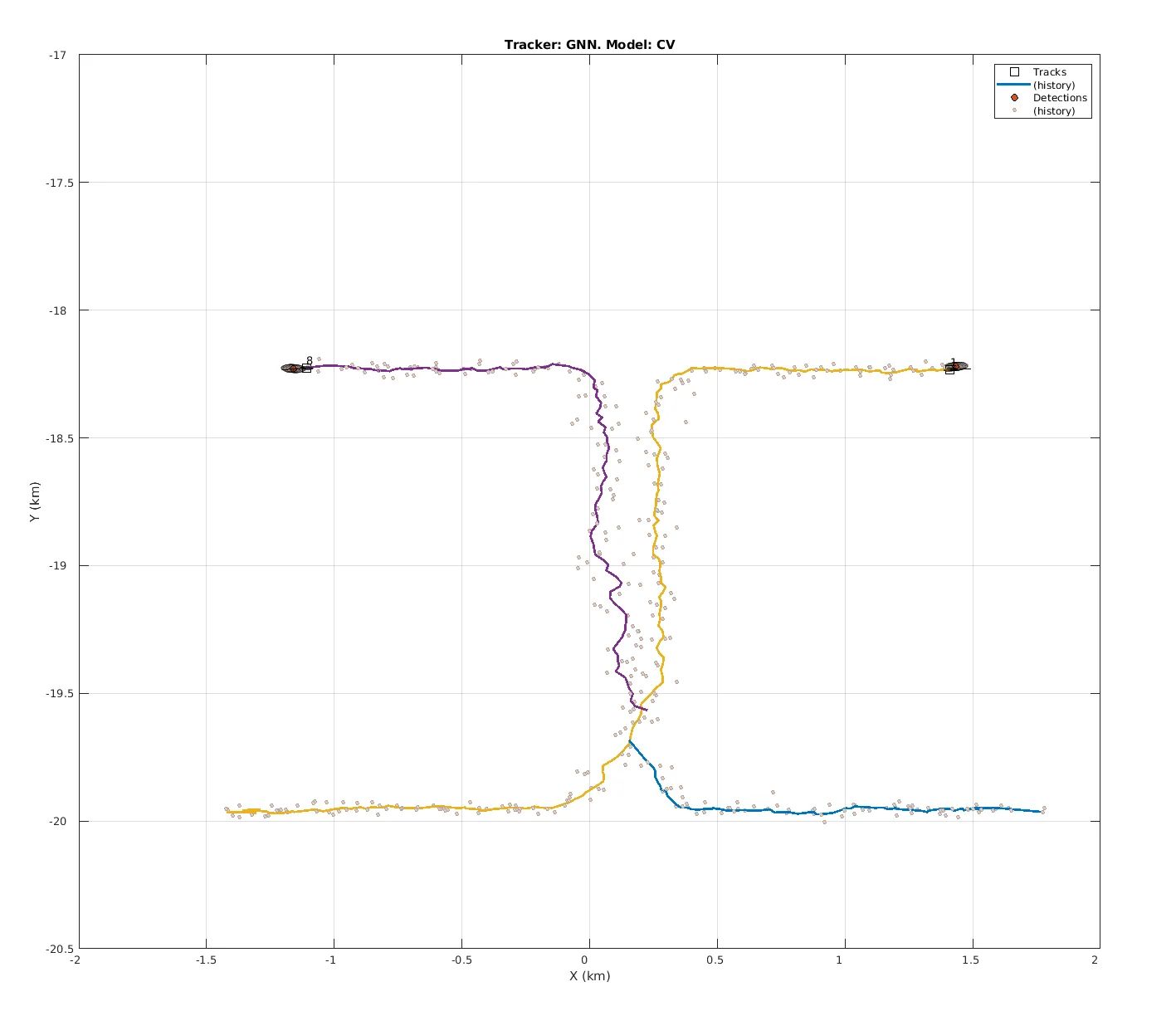
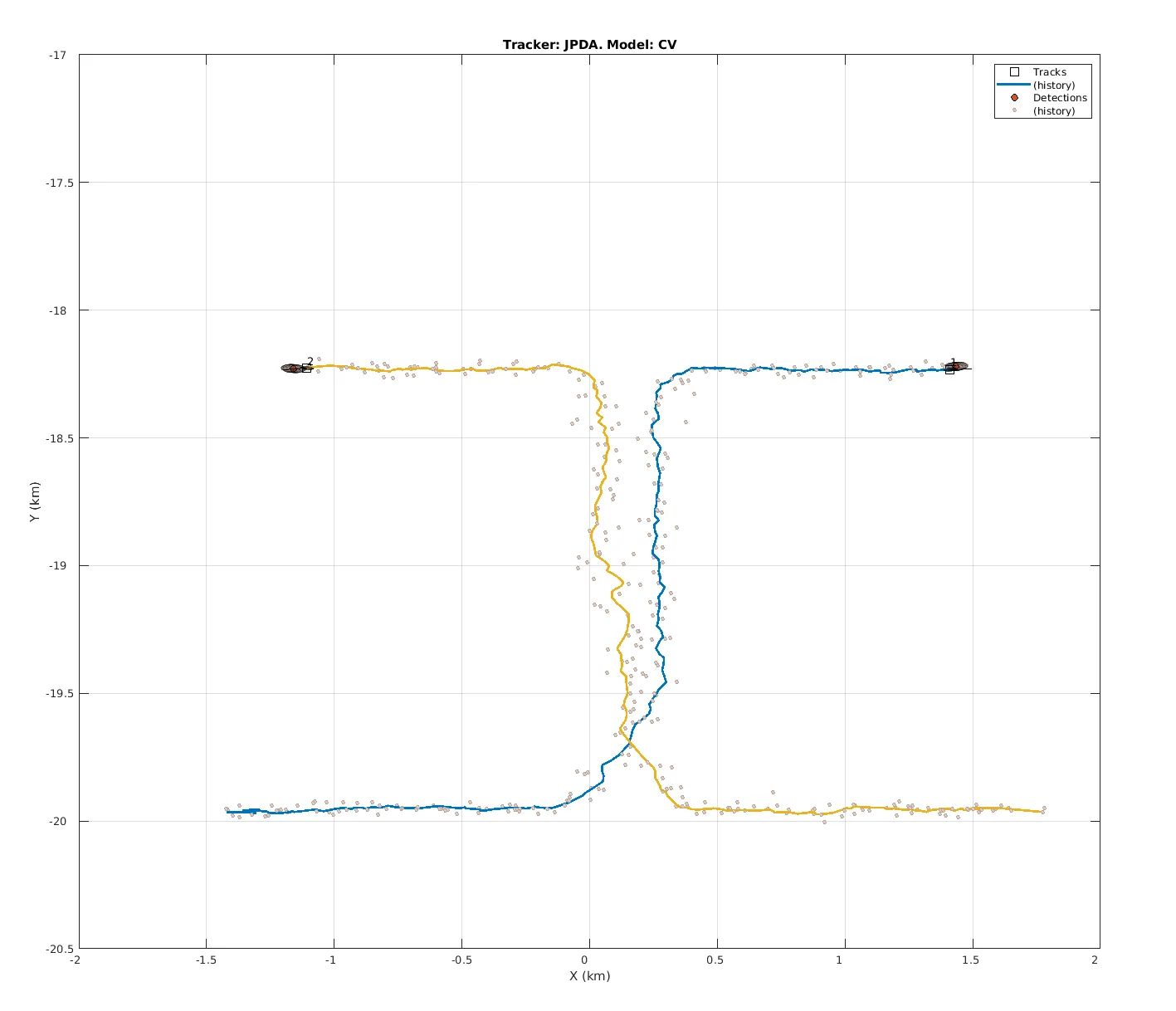
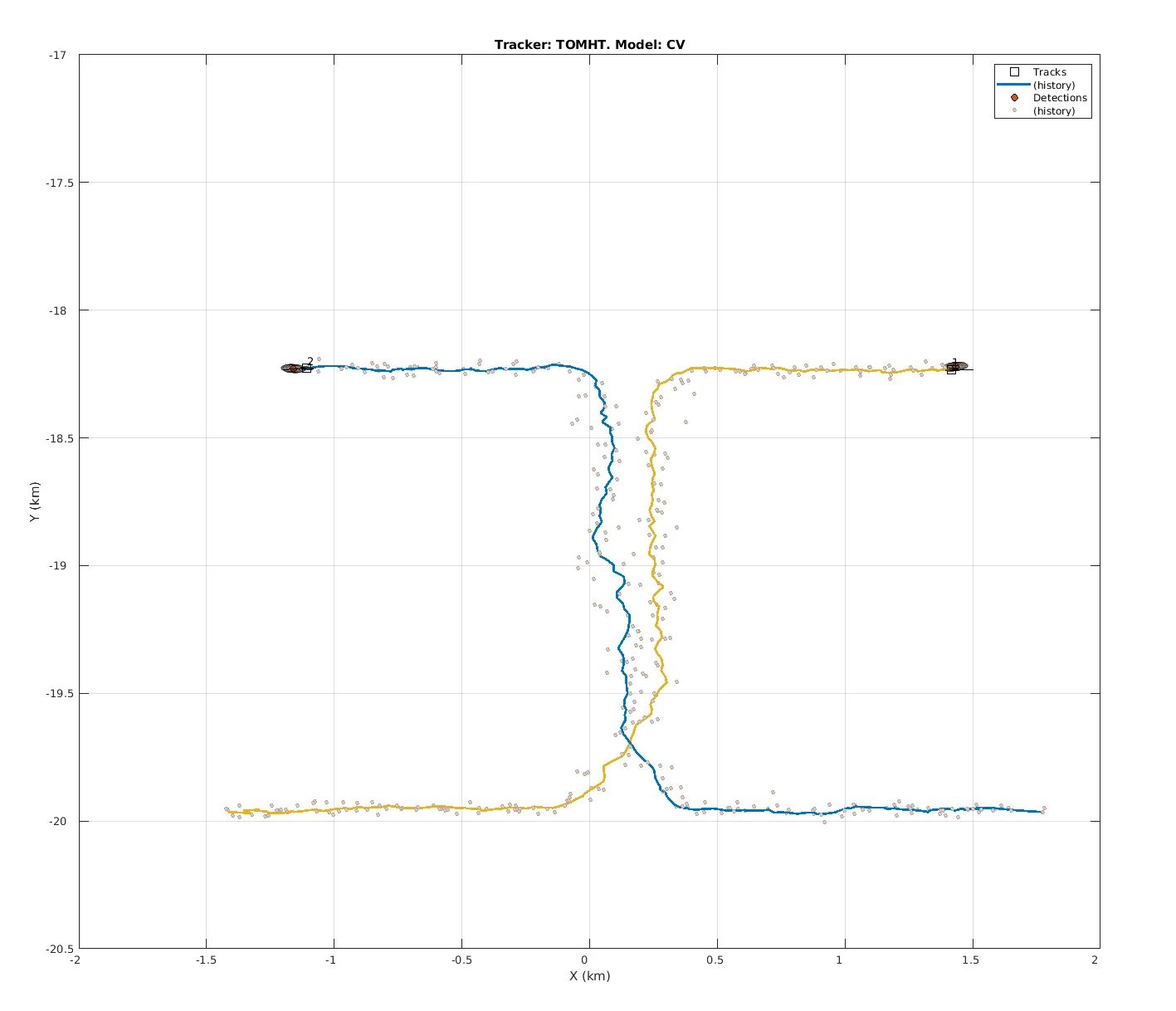
The graphs show three of the most common MOT algorithm, i.e. GNN, JPDA, TOMHT, and the different ID assignment as indicated by the different coloured lines. The simulation code can be found here: https://www.mathworks.com/help/fusion/ug/tracking-closely-spaced-targets-under-ambiguity.html
There are more advance algorithms such as PMBM, which is a Random Finite Set based method, and Graph based methods. My focus and the results of this document is based on the graph Bayesian methods, but I would introduce random finite set briefly as well.
This field usually investigate with Monte Carlo simulations and there are few well known characters of the filters. 1. Repulsion of MHT 2. Coalescing of JPDA 3. Spooky effect of CPHD. One of the issue is clearly multi-modality of the distribution. It can be treated with either MHT or particle filter. Recent analysis seems to suggest that particle filter is the way to go.
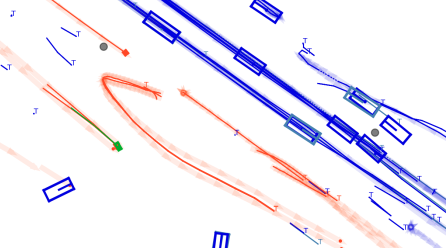
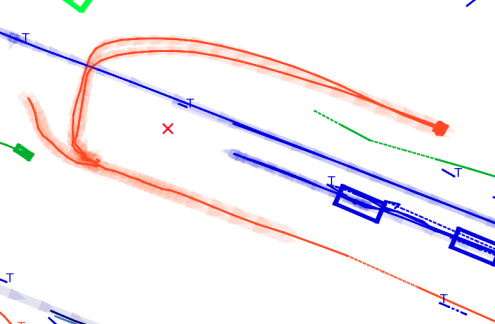
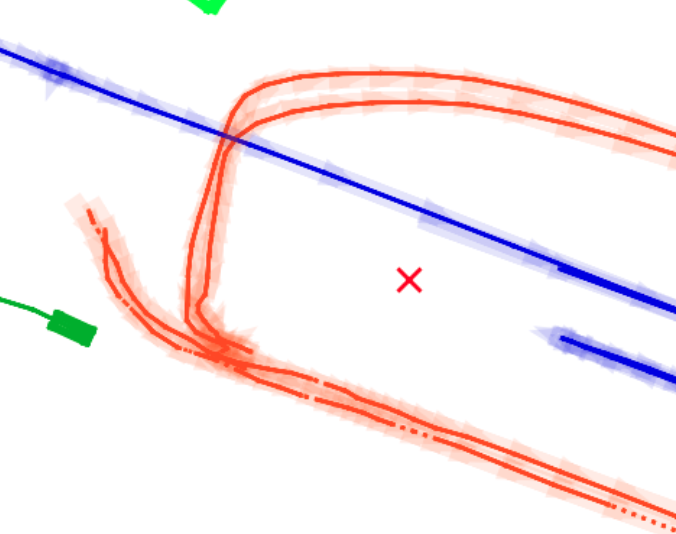
Here are some experiments result of different filters on the same dataset. This is the MHT filter, you can observe an abrupt change of the track, because multiple hypothesis are kept in the background.
This is the same tracking scene of global nearest neighbors. Keep in mind that this dataset has highly accurate Lidar detection with error in the centimeter level.
Here is the comparison between PMB and GNN, we can clearly see the tracks merging in PMB filter.
This side are the results of GNN filter over the same scene.
Random Finite Set
This picture is taken from Prof. Silvia Ferarri's presentation. Random Finite Set (RFS) is a mathematical formalism utilized to address the uncertainty in cardinality that arises in Multi-Object Tracking problems. Specifically, variations in cardinality are integrated into the dynamics of the set, and Bayesian recursion is carried out via set integration. Notably, the first moment within this framework is interpreted not as the expected value but as the cardinality. This approach is fascinating because it demonstrates how theories can be expanded to include additional considerations while still adhering to established constraints of an axiom system.
Prof. Peter Willett asked some profound question a decade ago regarding RFS: Since cardinality acts as a constraint on the optimization problem, how do trackers perform when these constraints are removed? The implication is that performance shouldn't worsen without the constraints, but the critical inquiry is whether it can improve.
As a side note, I find Silvia's work one of the better ones out there. Her idea of extracting information out of negative detection is a very good one. Her book, Information Driven Control, is one of my favorite.
The more comprehensive treatment of RFS can be found in the following. Personally I find Kay's book and Mahler's book, as well as the AESS distinguished lecture series helpful.
There is some sort of champagne to push PMBM forward. I can understand the impetus from a career making perspective. It is, in its essence, a kitchen sink approach to things. A fun toy to play with always.
2. Multitarget Bayes Filtering via First-Order Multitarget Moment.
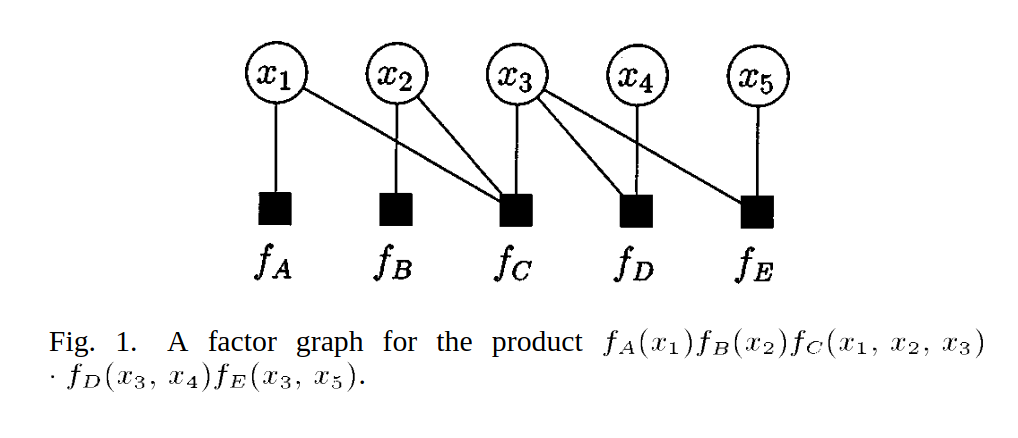
Factor Graphs and the Sum-Product Algorithm
The analysis is based on this tutorial on Factor Graphs and the Sum-Product Algorithm.
Belief Propagation(BP), a.k.a Sum-of-Product(SoP), is known for its fast computation, and has increasingly find its way into various applications.
Single Marginal Probability:
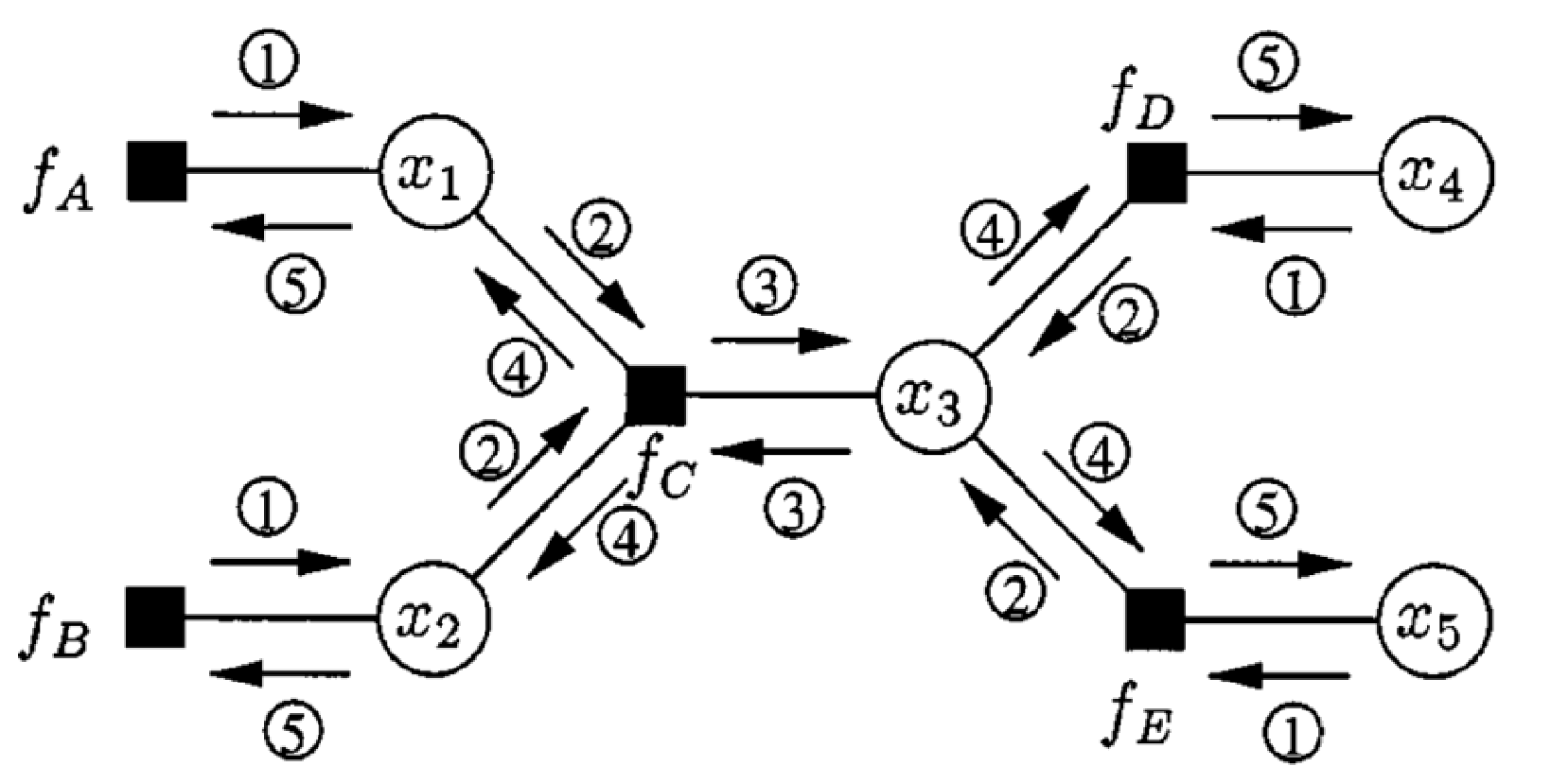
The squares represent local function, the circles represent variable. Figure 1 represent this joint probability :
For marginal probability for x1:
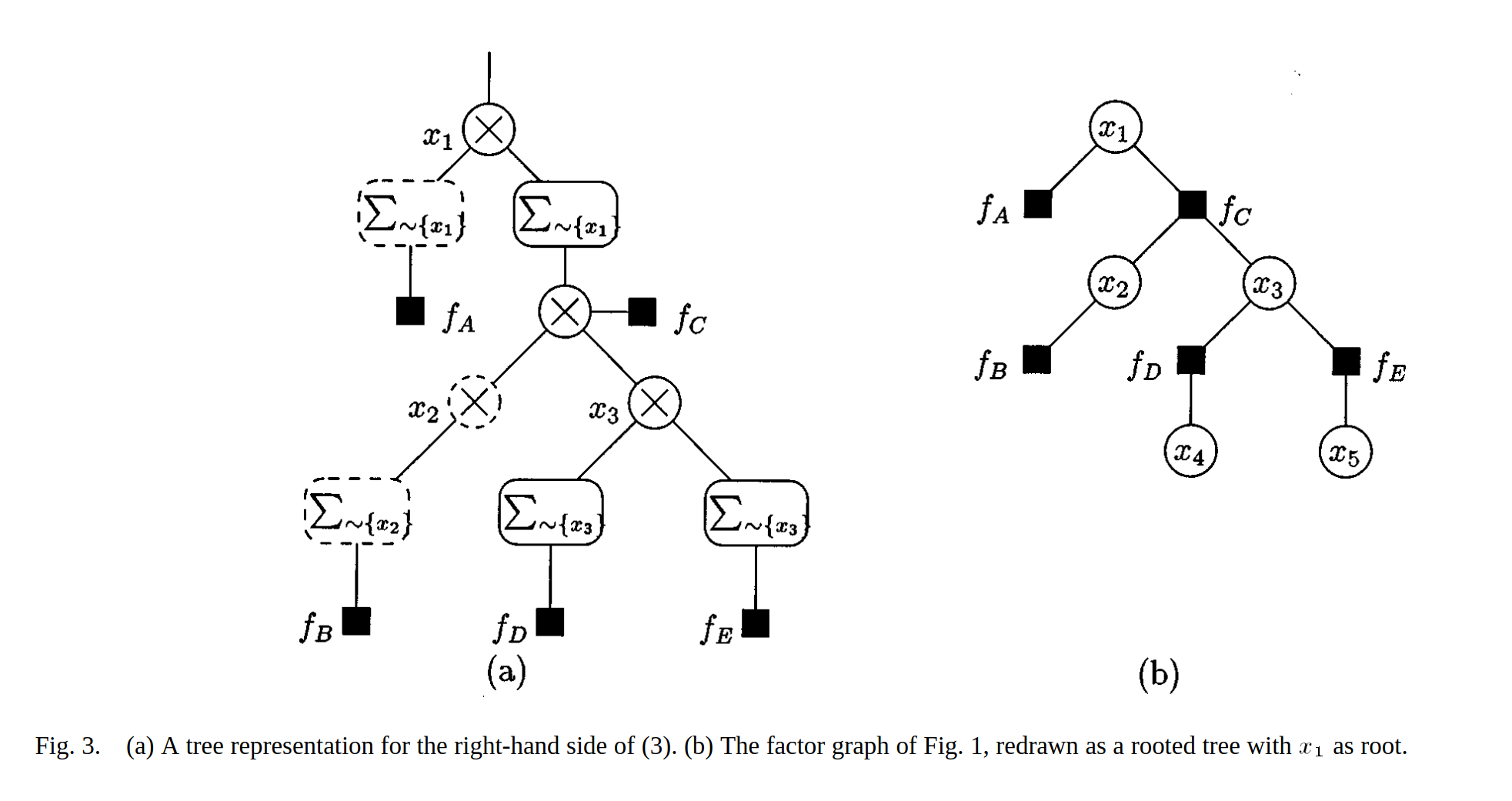
This marginal probability can be represented by a tree graph with x1 as the root of the tree:
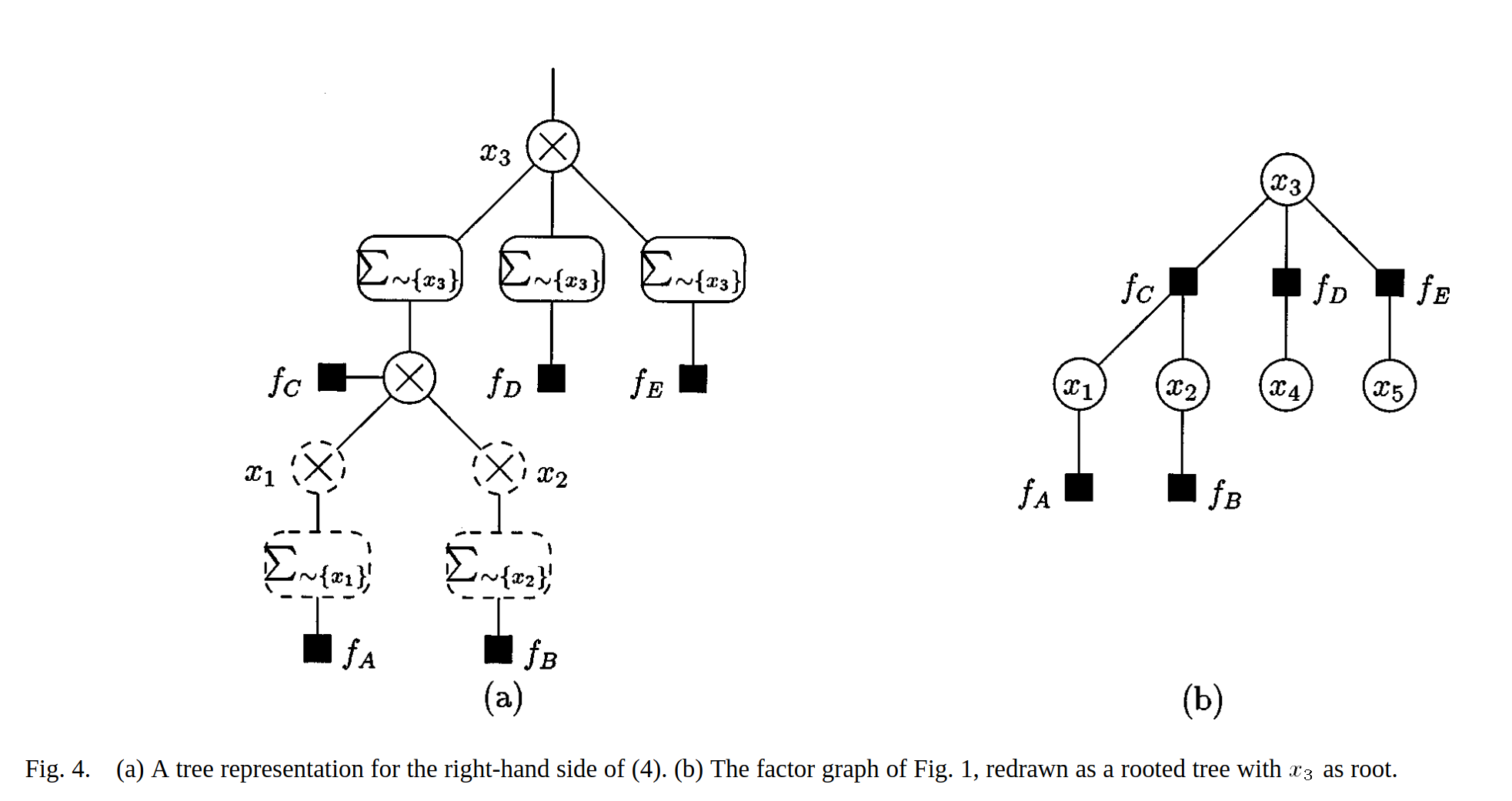
Similarly, the marginal probability for x3 is the following expression:
This marginal probability can be represented by a tree graph with x3 as the root of the tree:
All Marginal Probabilities:
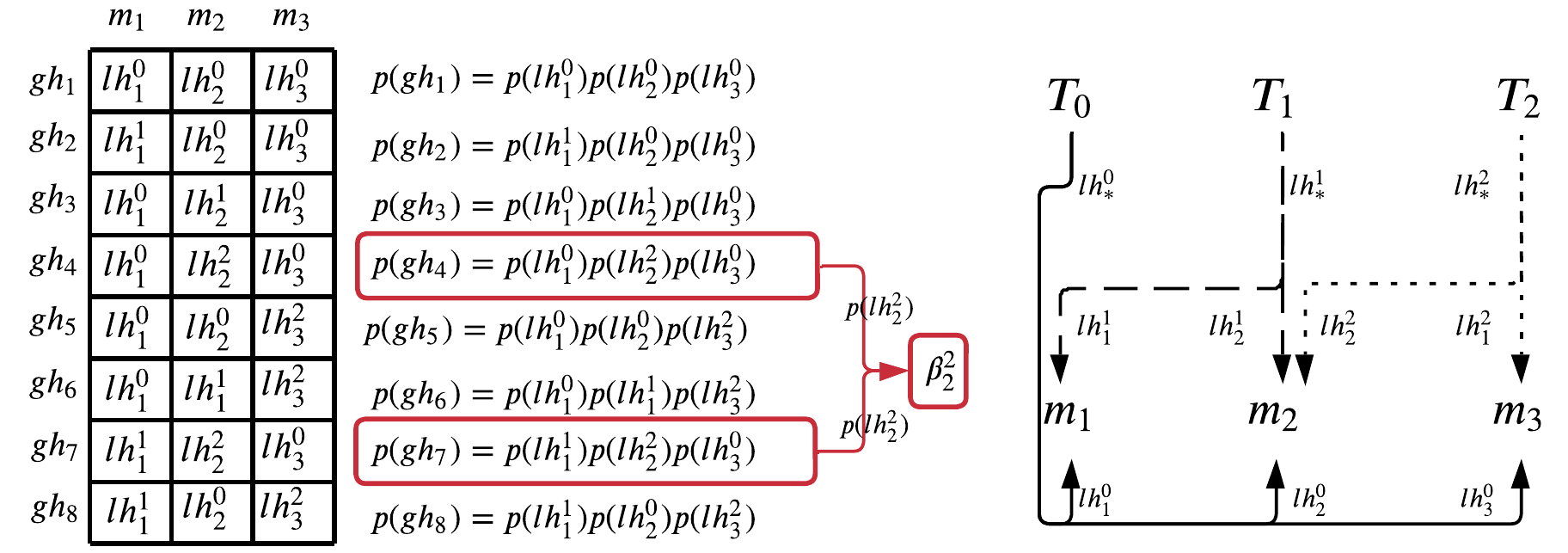
In many circumstances, we may be interested in computing more than one value of marginal probability. Such computations could be achieved by applying a single algorithm separately for each desired value of g(x) However, this approach is unlikely to be efficient because many of the sub-computations performed for different values of g(x) will be identical.
Computation for all values can be efficiently accomplished by essentially 'overlaying' all possible instances of the single algorithm on a single factor graph.
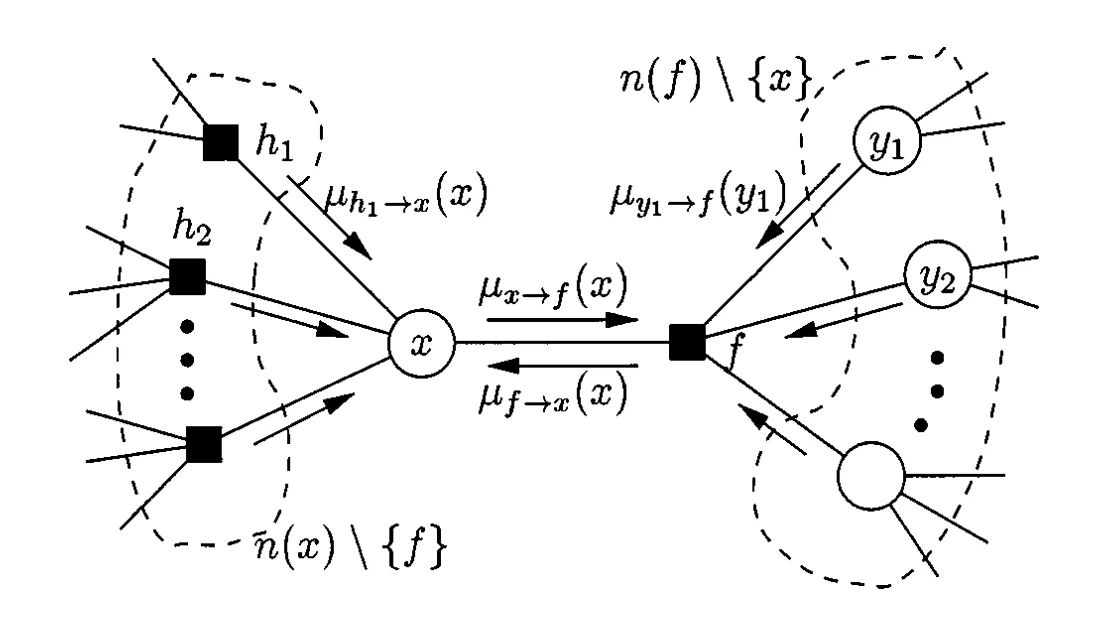
No particular vertex is taken as a root vertex, so there is no fixed parent/child relationship among neighboring vertices. Instead, each neighbor w of any given vertex v is at some point regarded as a parent of the vertex v. The message passed from vertex v to w is computed just as in the single algorithm, i.e., as if were indeed the parent of and all other neighbors of were children.
As in the single algorithm, message passing is initiated at the leaves. Each vertex remains idle until messages have arrived on all but one of the edges incident.
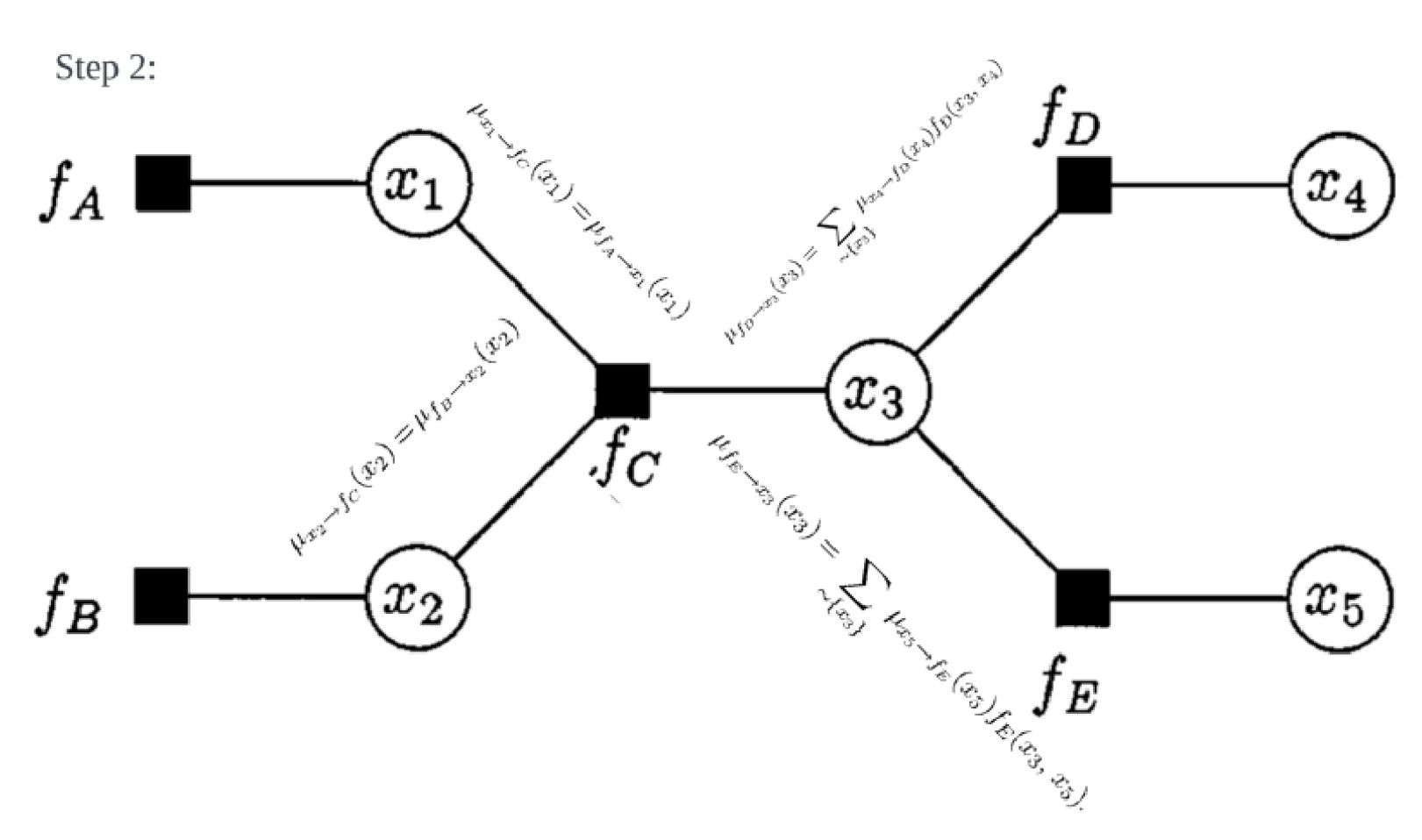
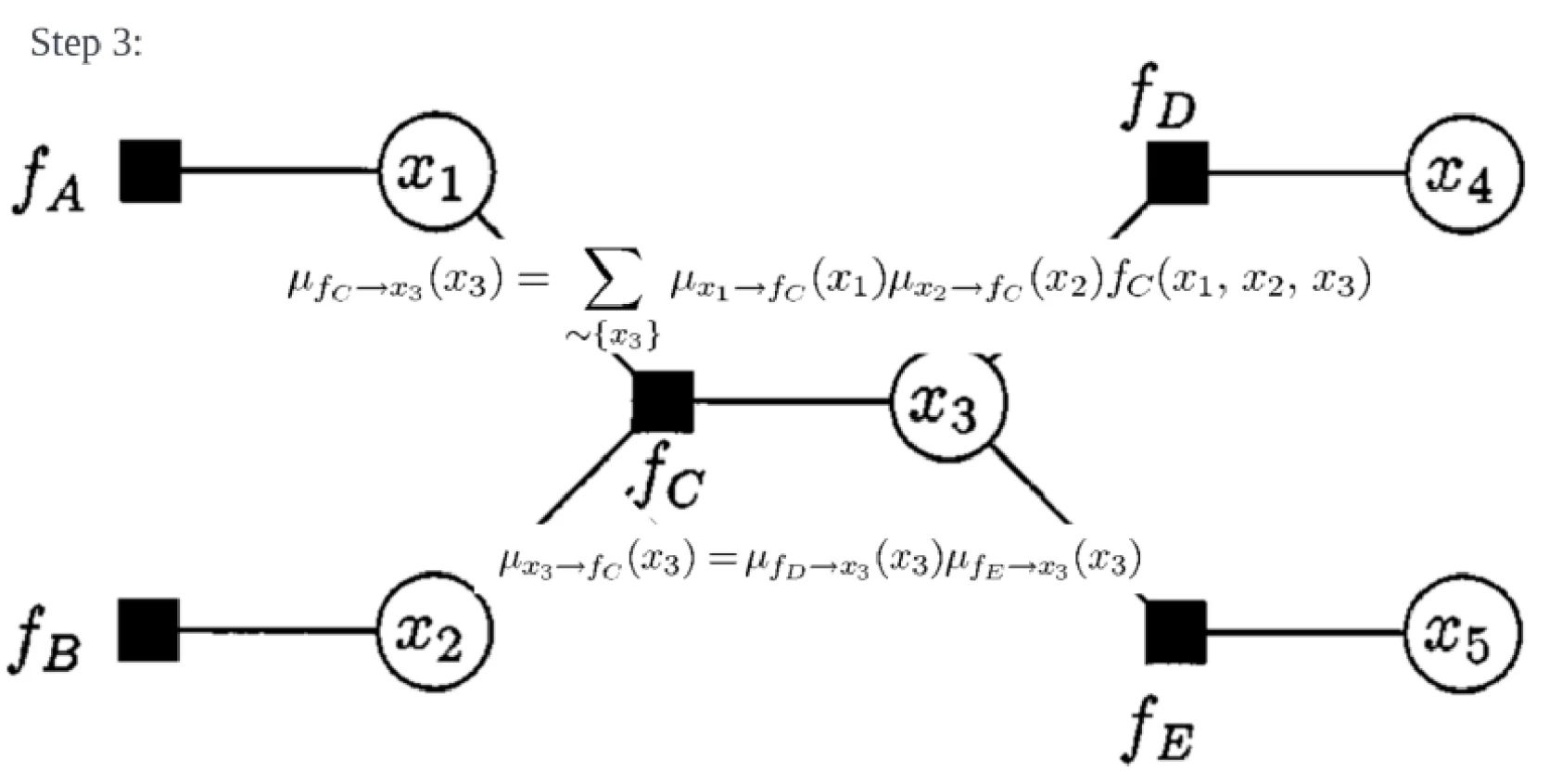
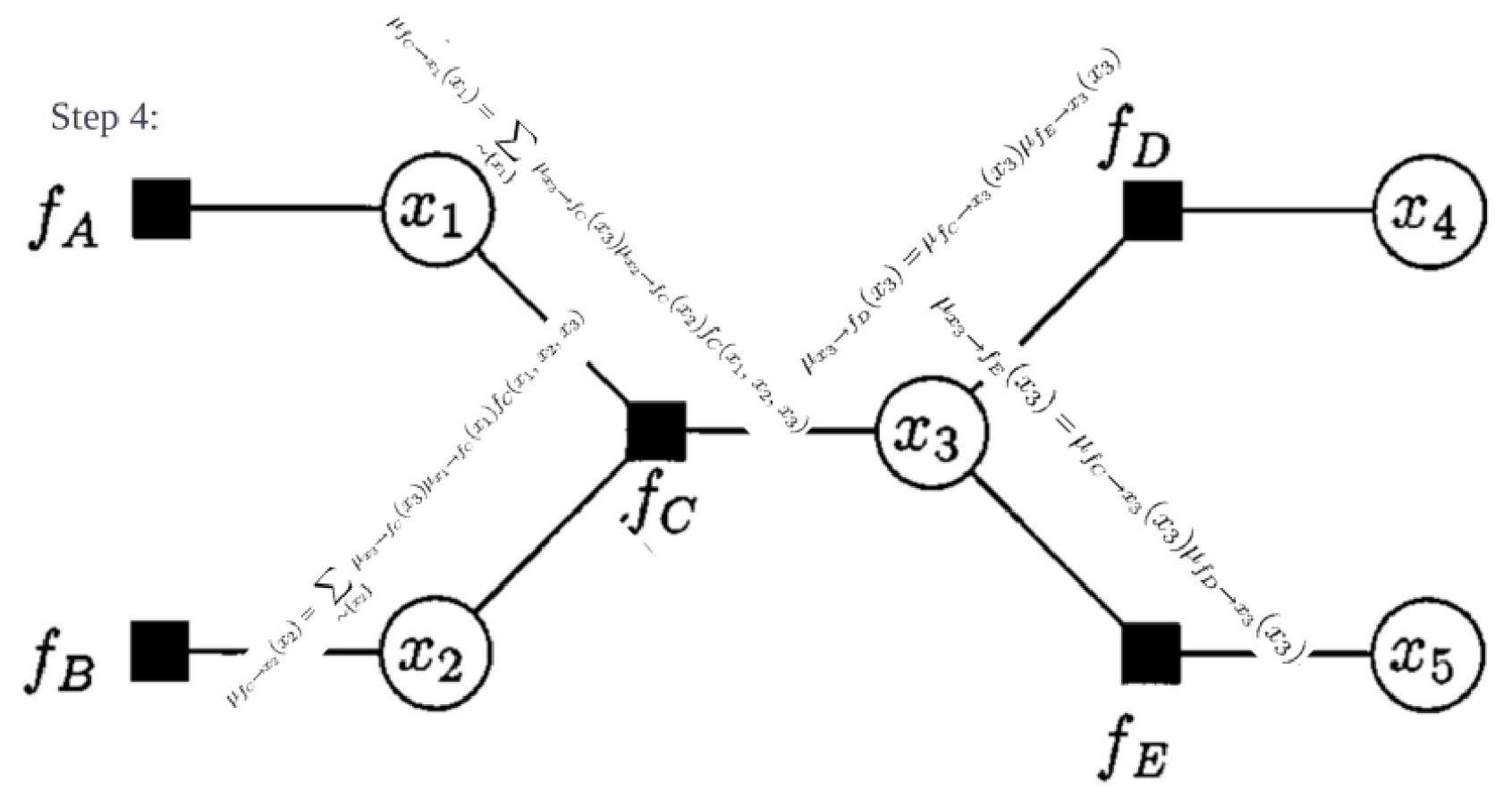
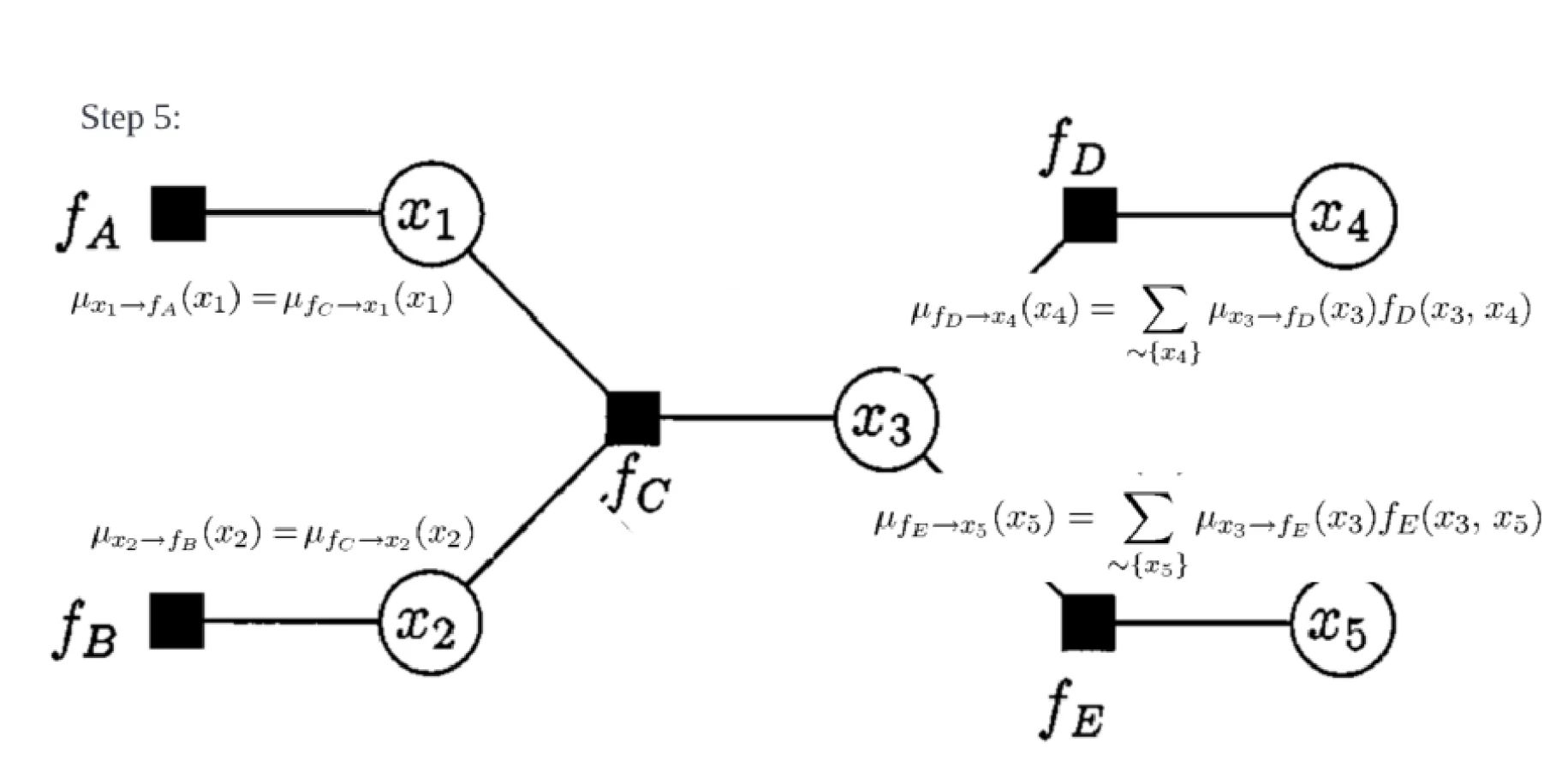
variable to local function:
local function to variable:
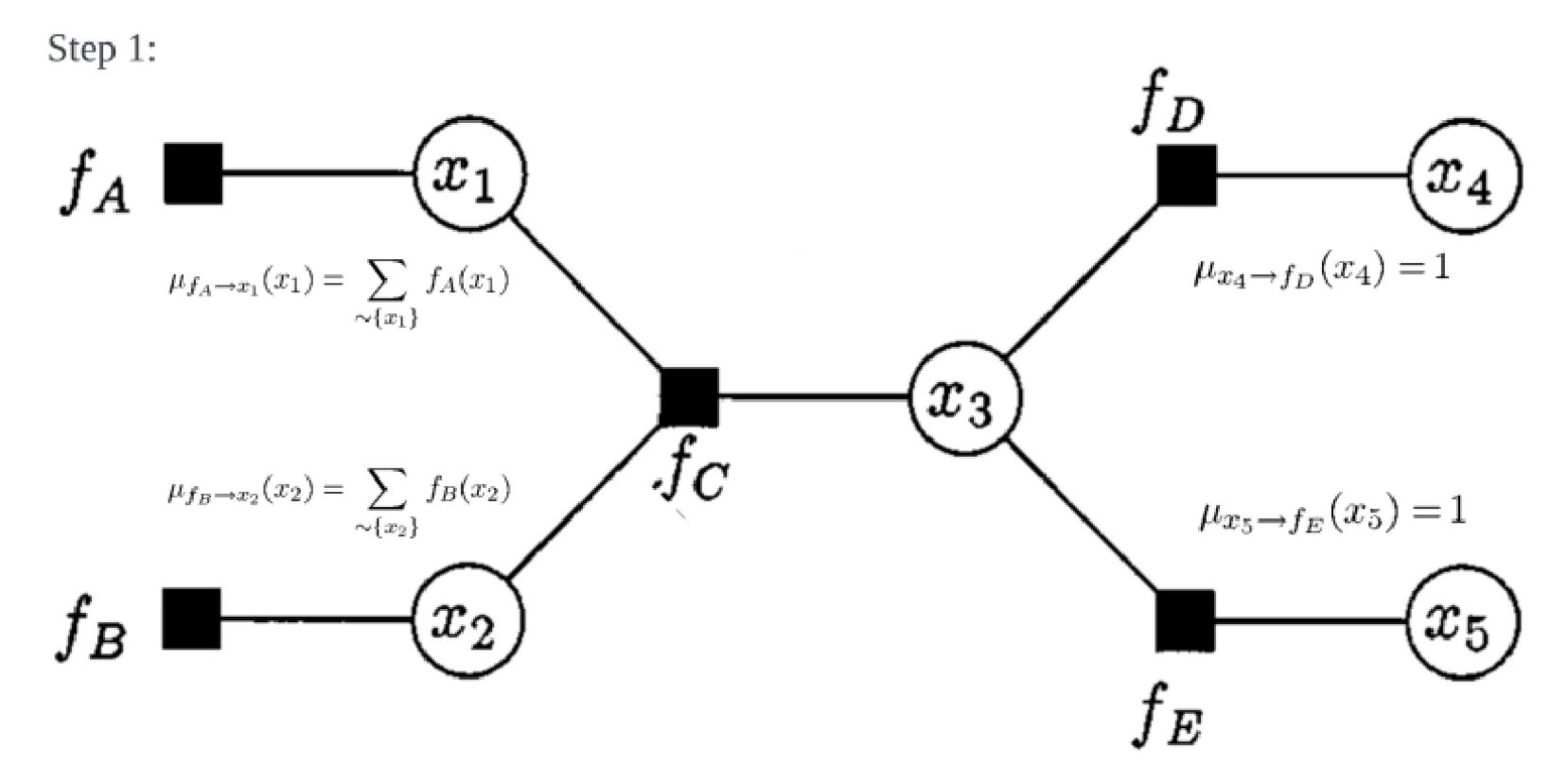
Example
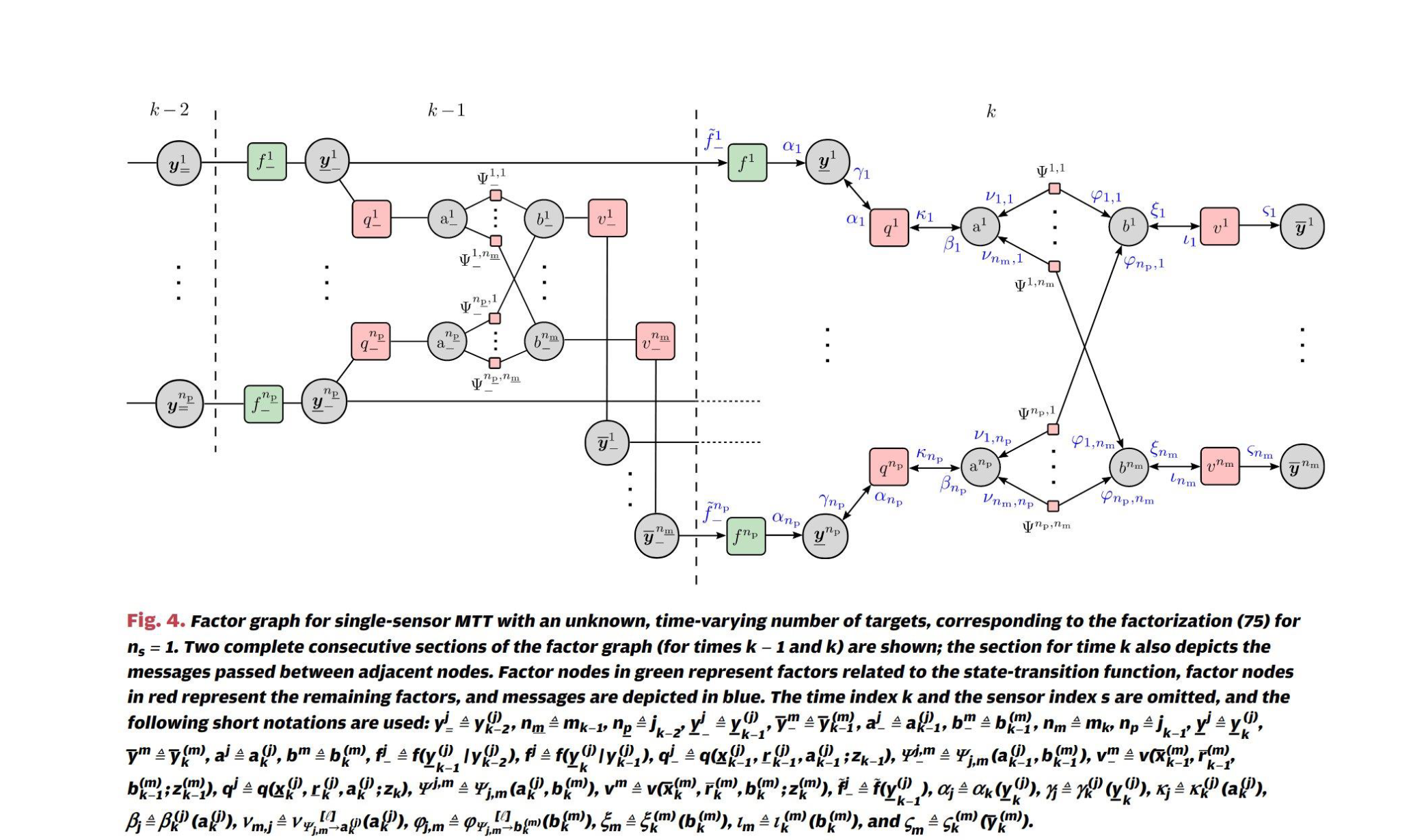
BP based Multi-object Tracking
The analysis is based on the works of Prof. Florian Meyer of UCSD. His works can be found here, and this is his presentation from a while back.
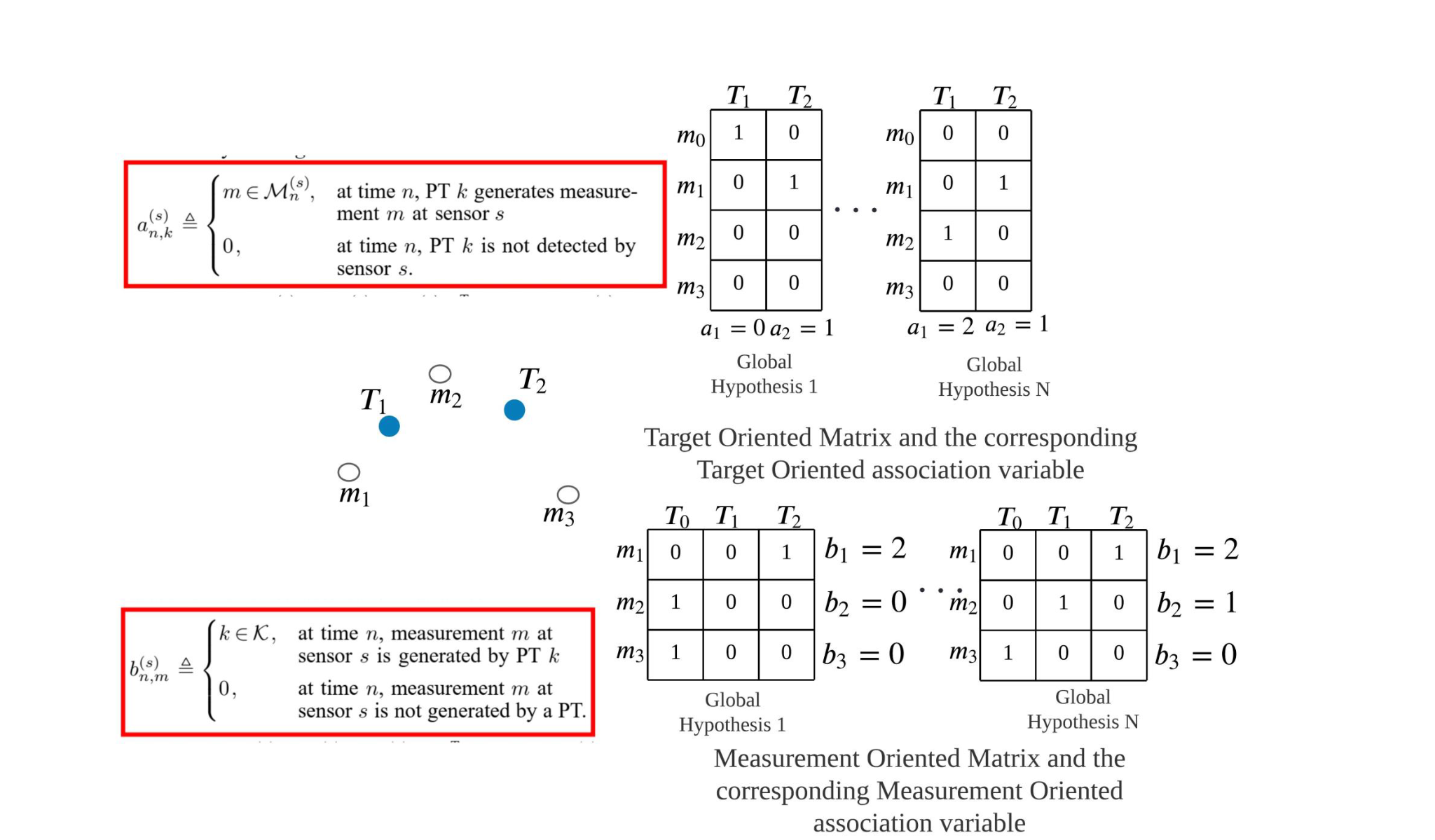
Why factor graph? The best way to see how the graph structure find its way into the marginal computation problem is probably through the JPDA computation. The marginal computation consists of a series of multiplication and summations, in certain order. That computation is expensive, and factor graph essentially provide a structured approximation to that exact computation. The ordering of the sum and multiplication is mapped to that structure, and the approximated computation is terminated when a terminal condition is met. The computation complexity scales linearly with the objects to be tracked, which makes factor graph an attractive option for many.
Joint pdf for the MOT problem:
The Likelihood Function:
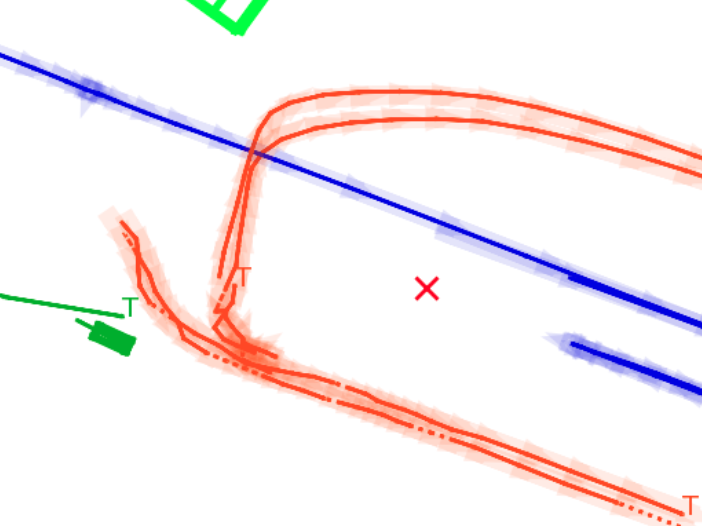
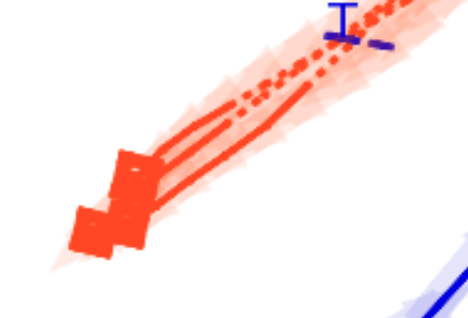
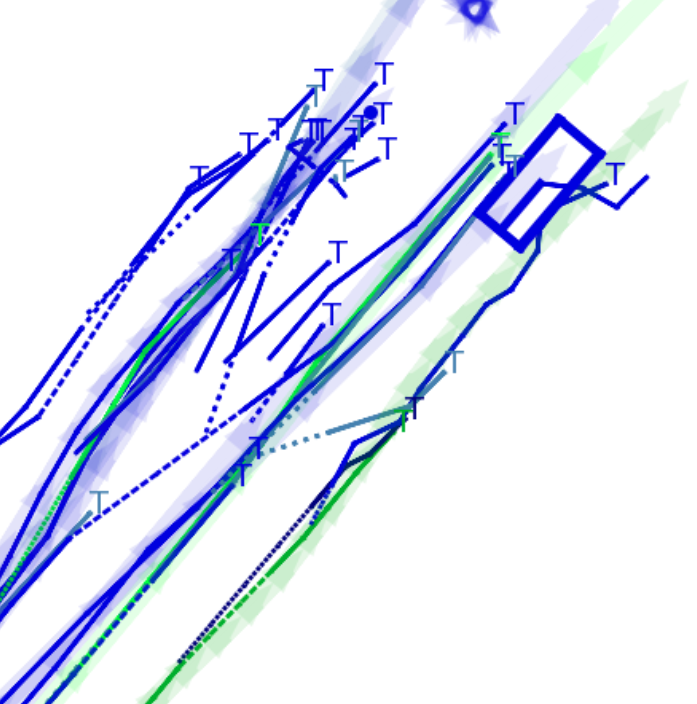
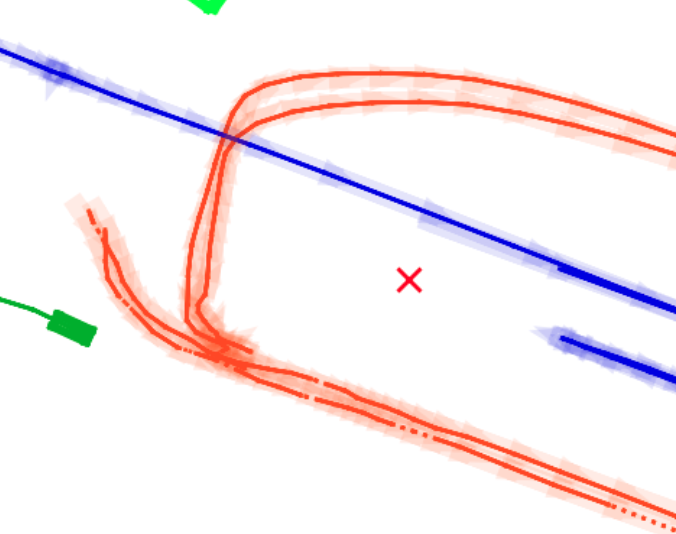
BP based Multi-object Tracking Results Visualization
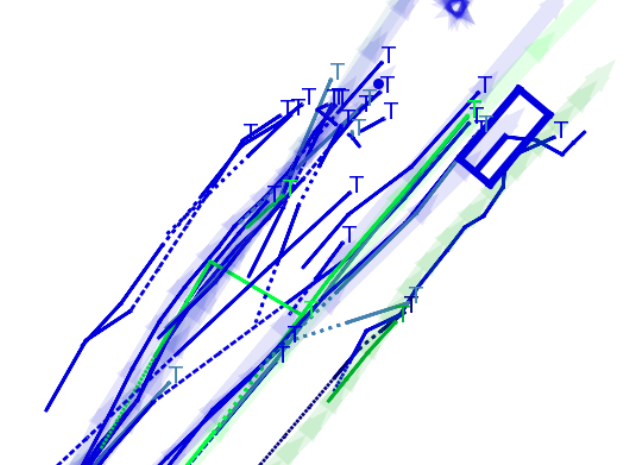
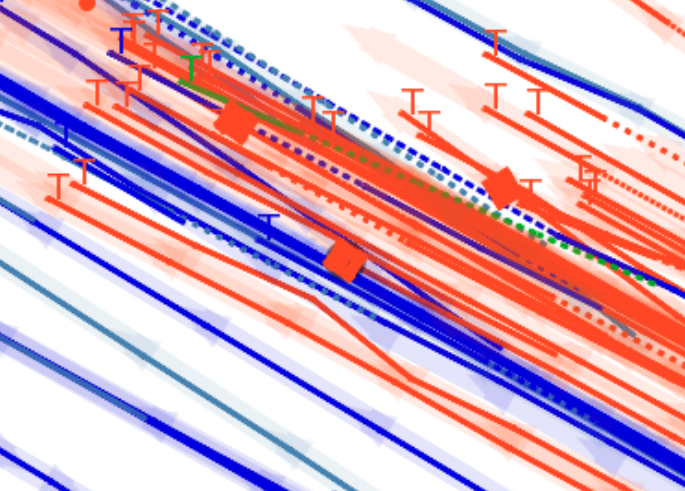
This visualization of graph based MOT for the nuScenes dataset. The dataset can be found here: https://www.nuscenes.org/ Use the sliding bar on the right side of this page to adjust frame numbers. There are total of 40 frames in this presentation.
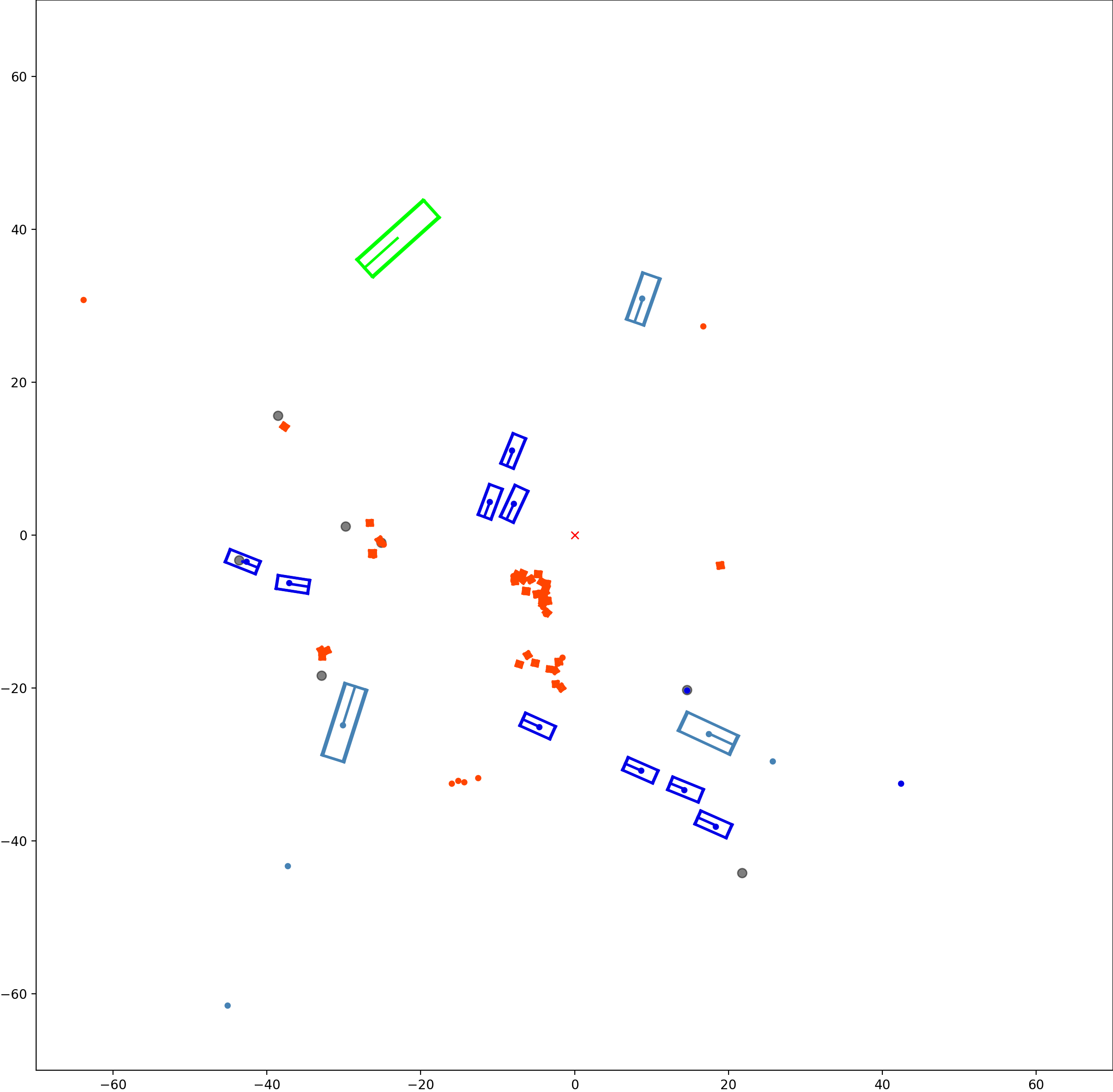

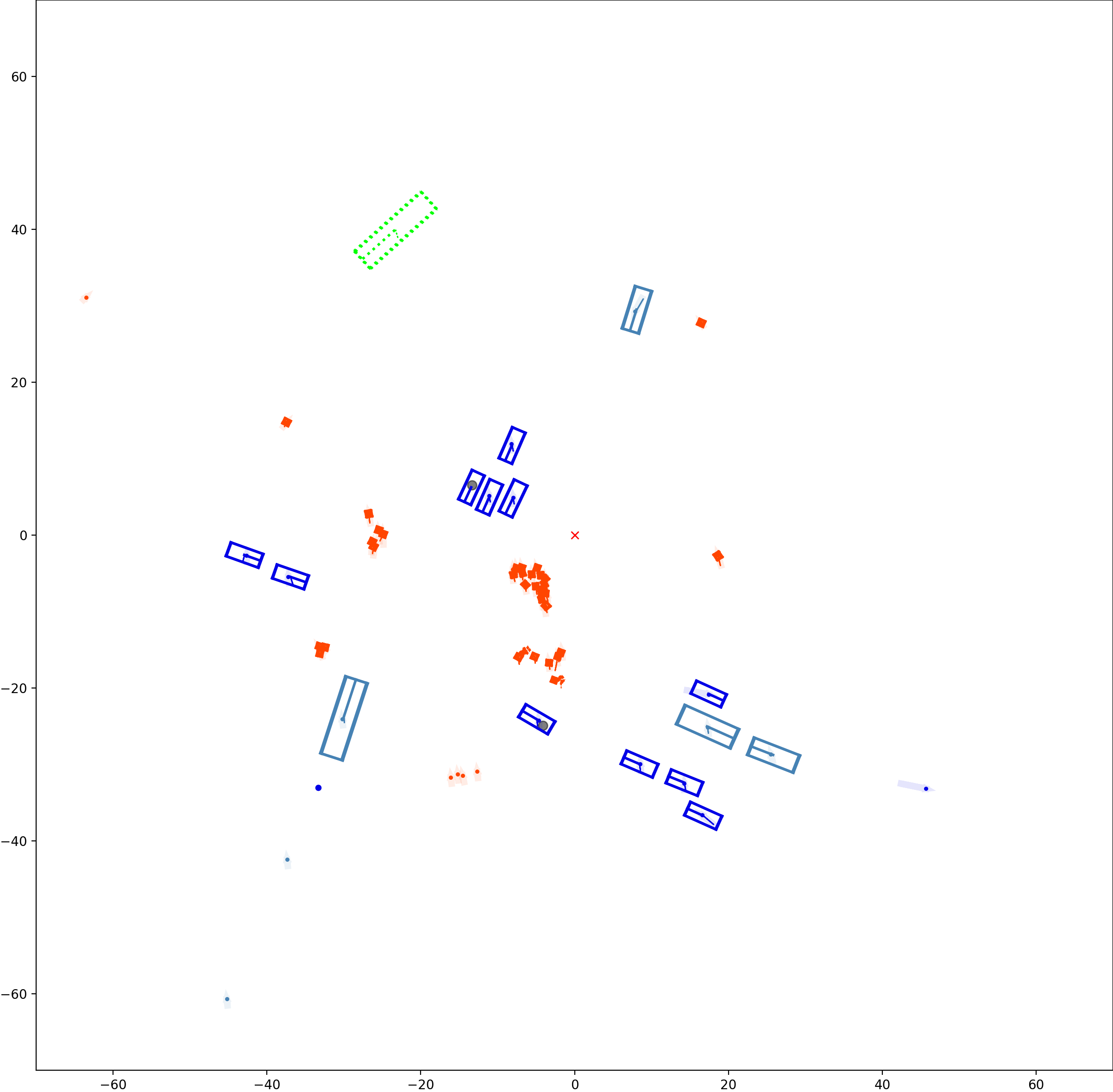
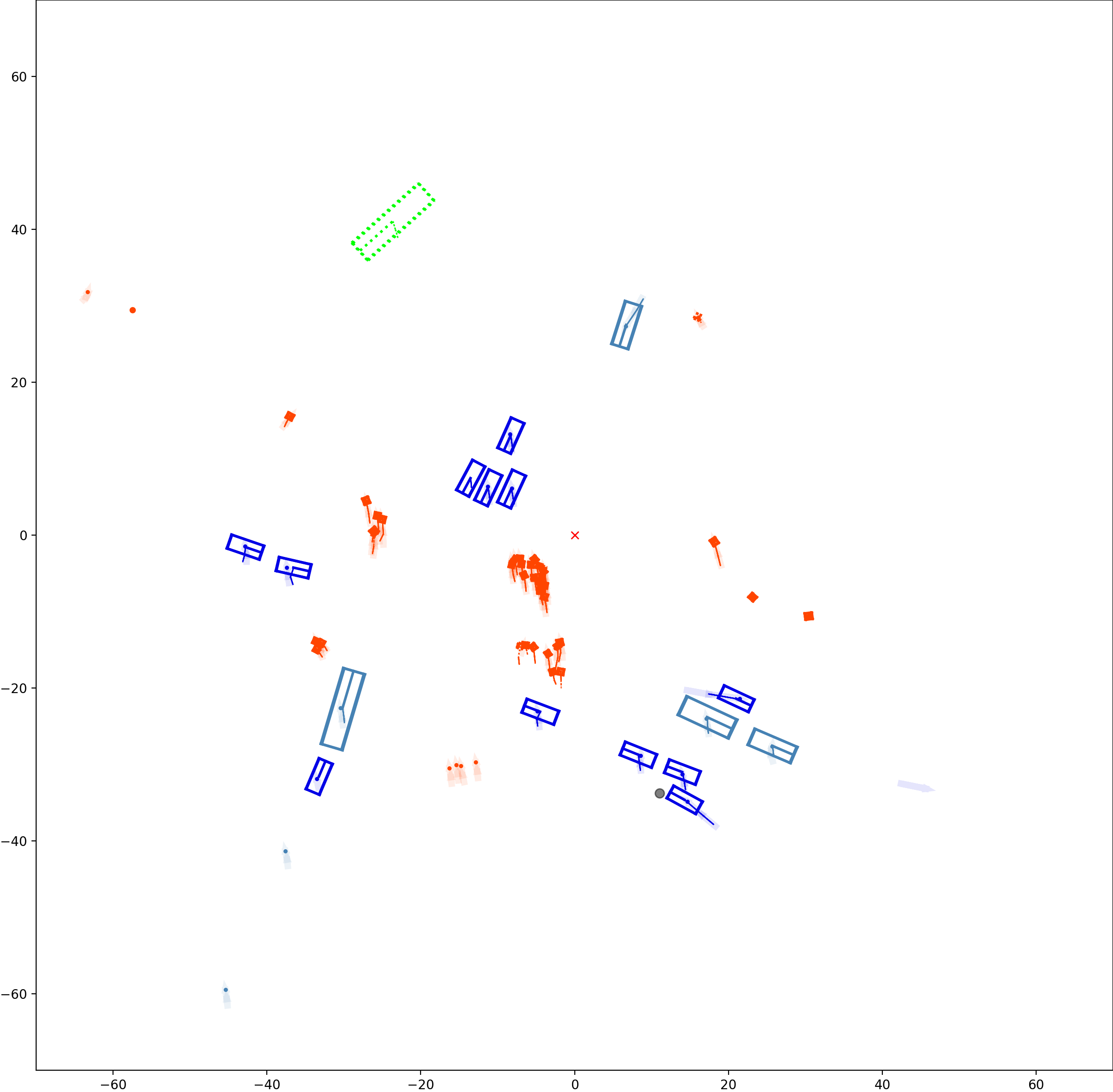
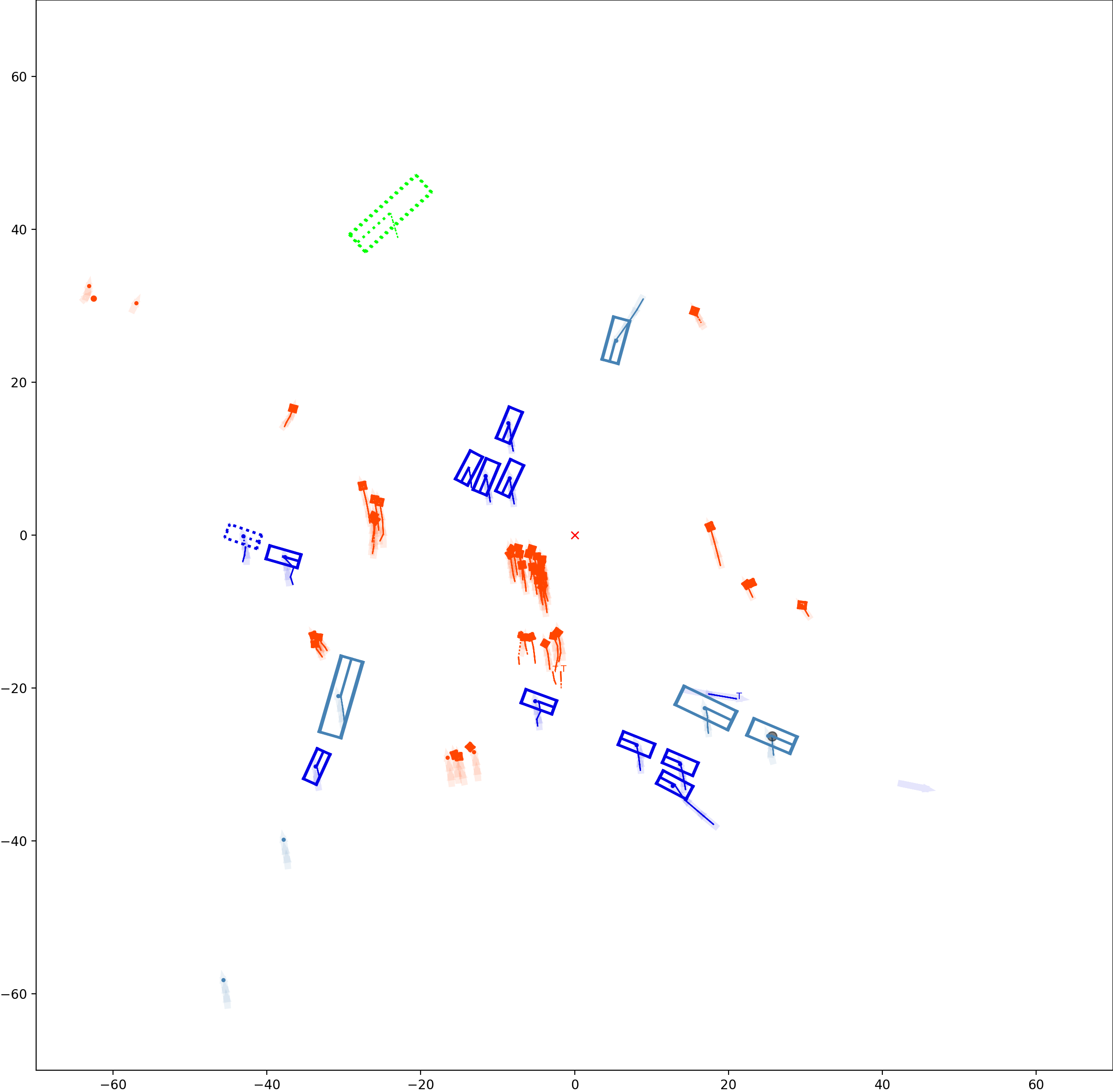
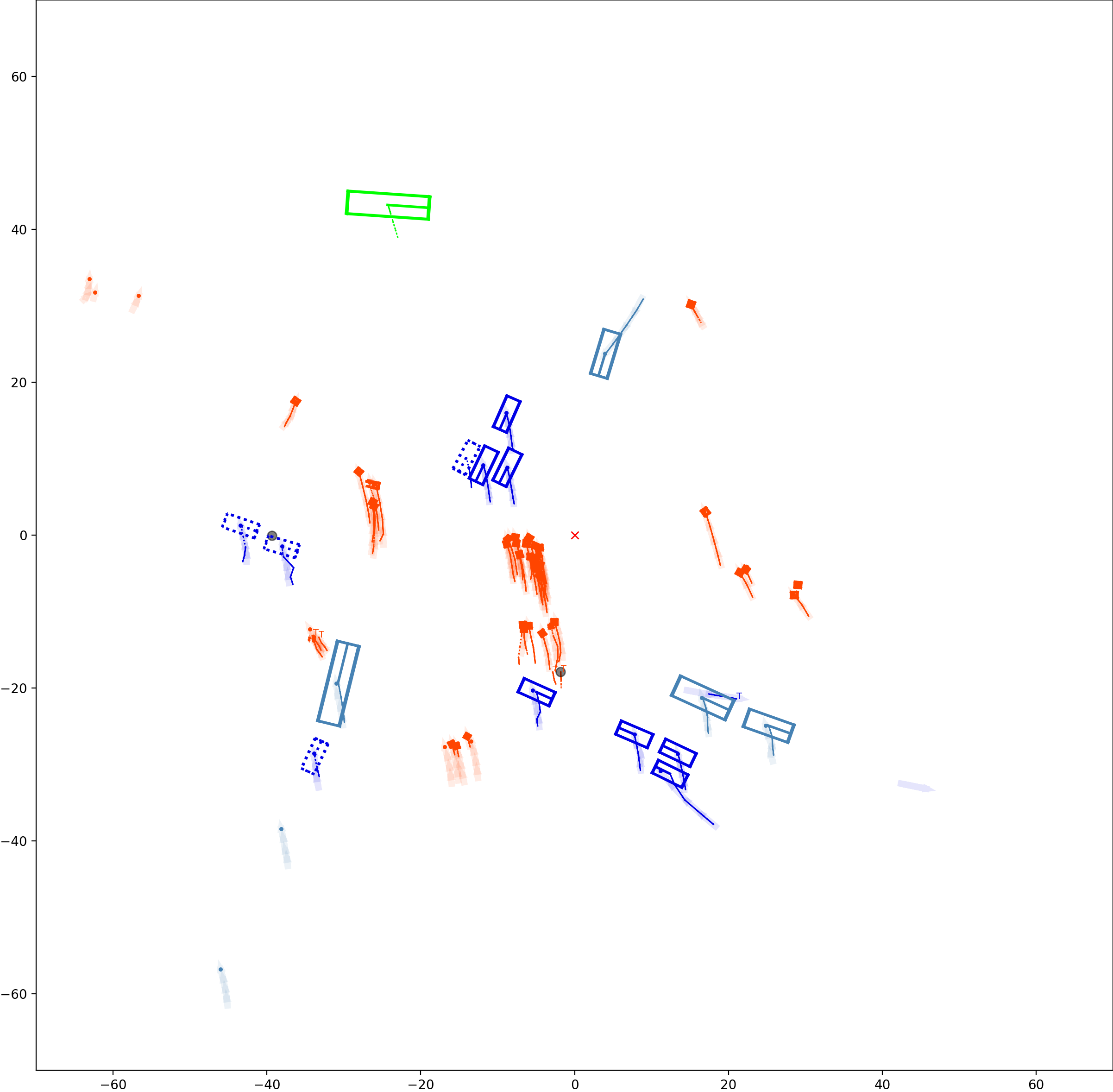
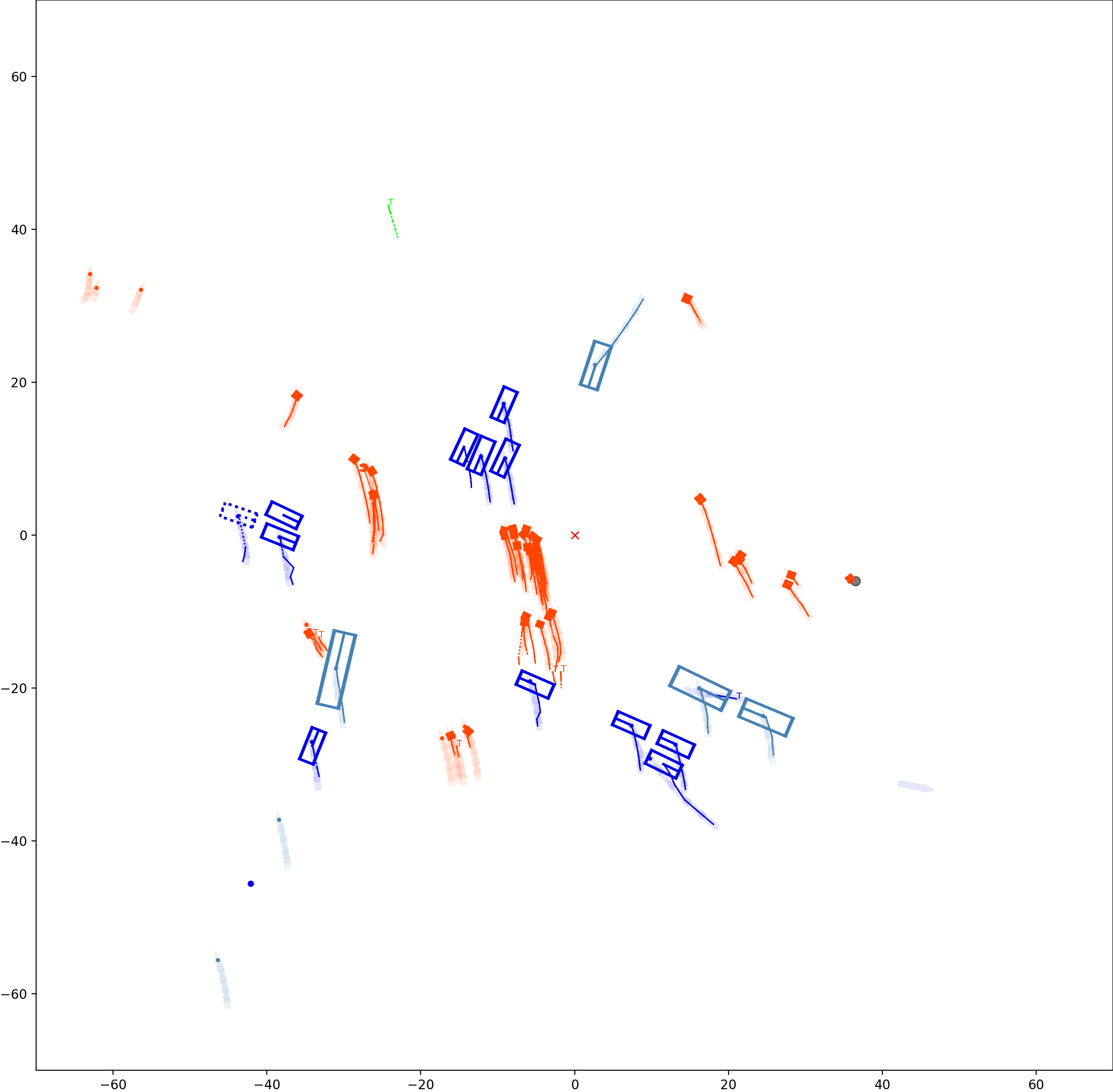
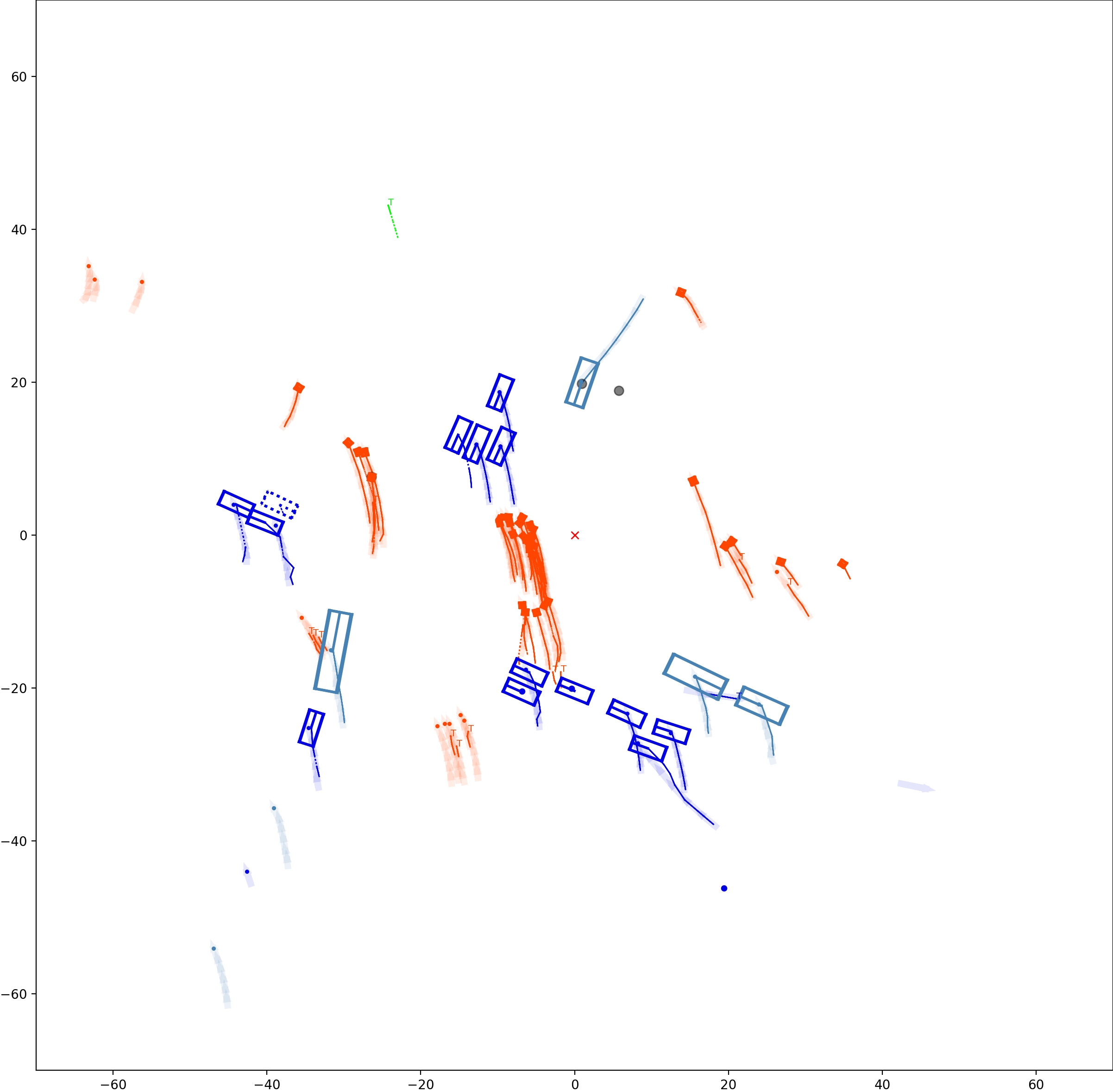
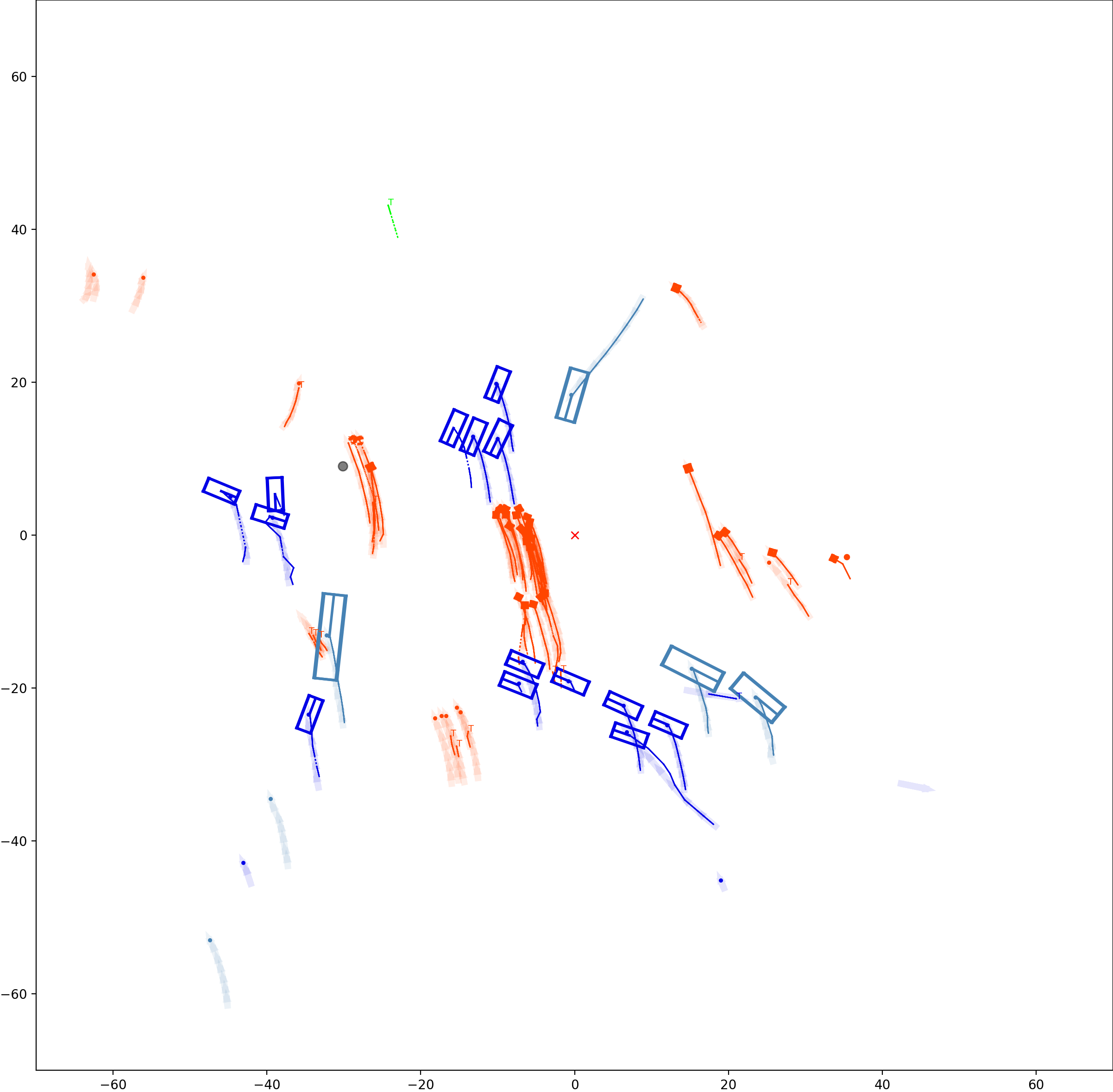
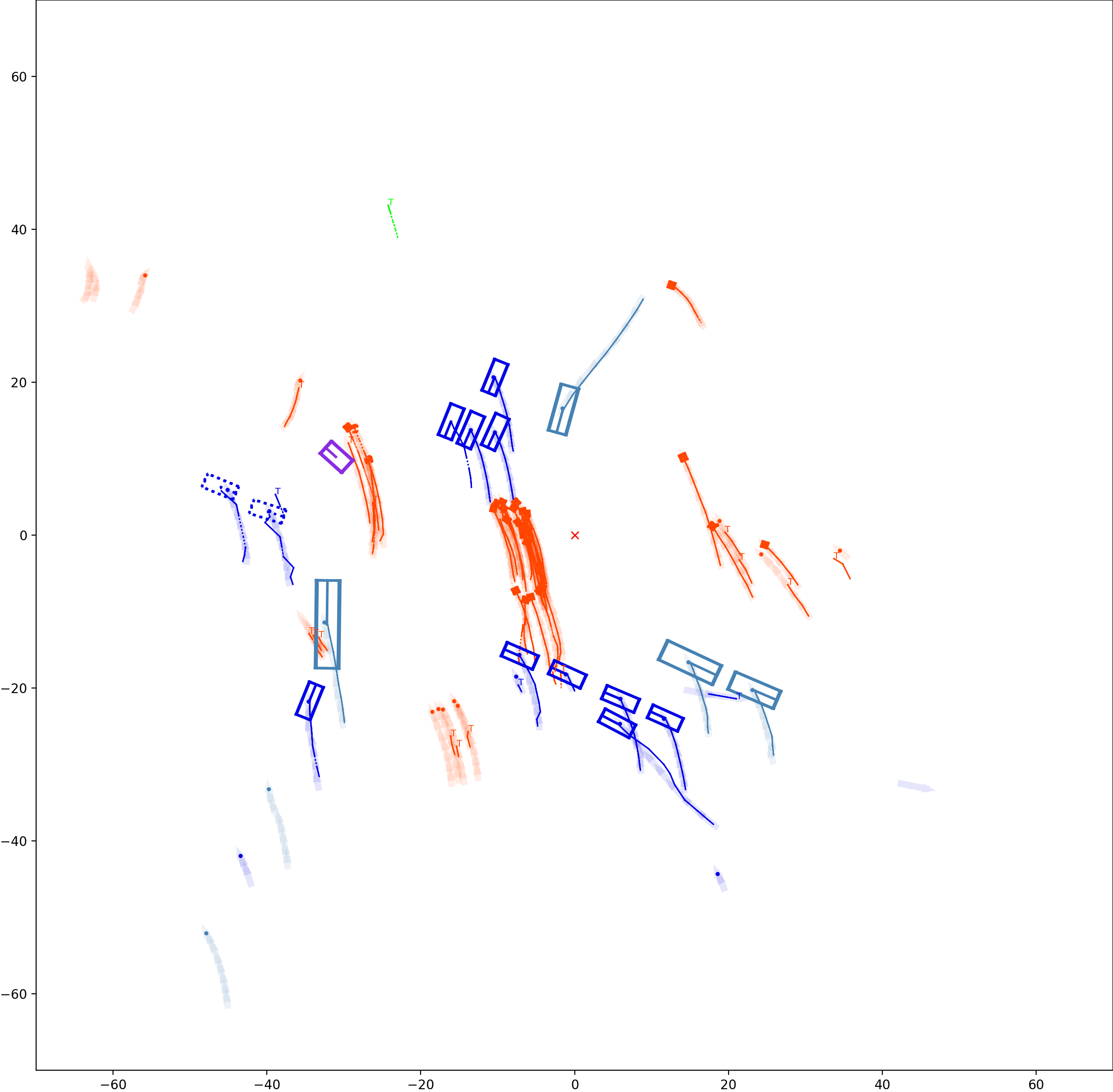
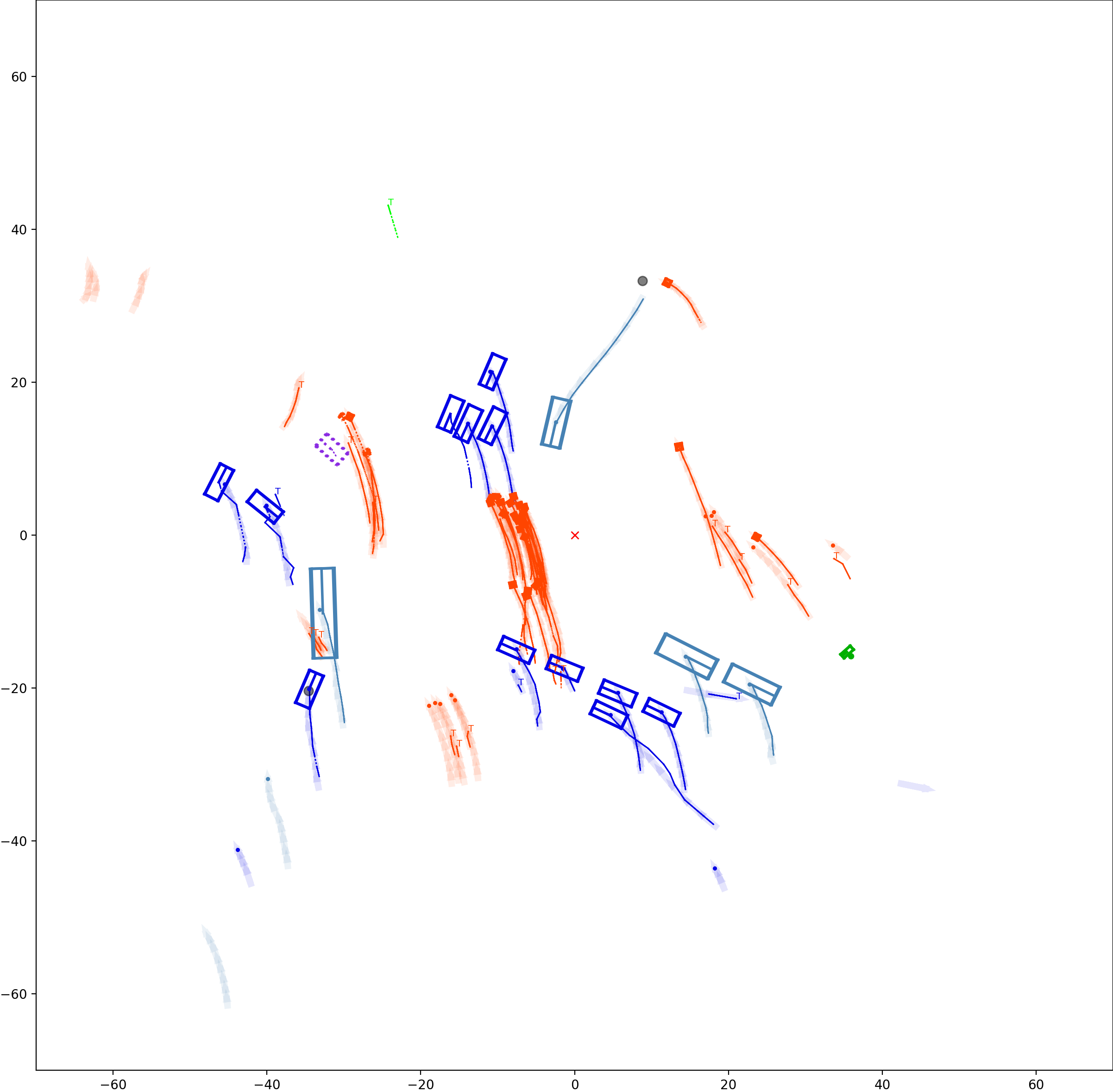
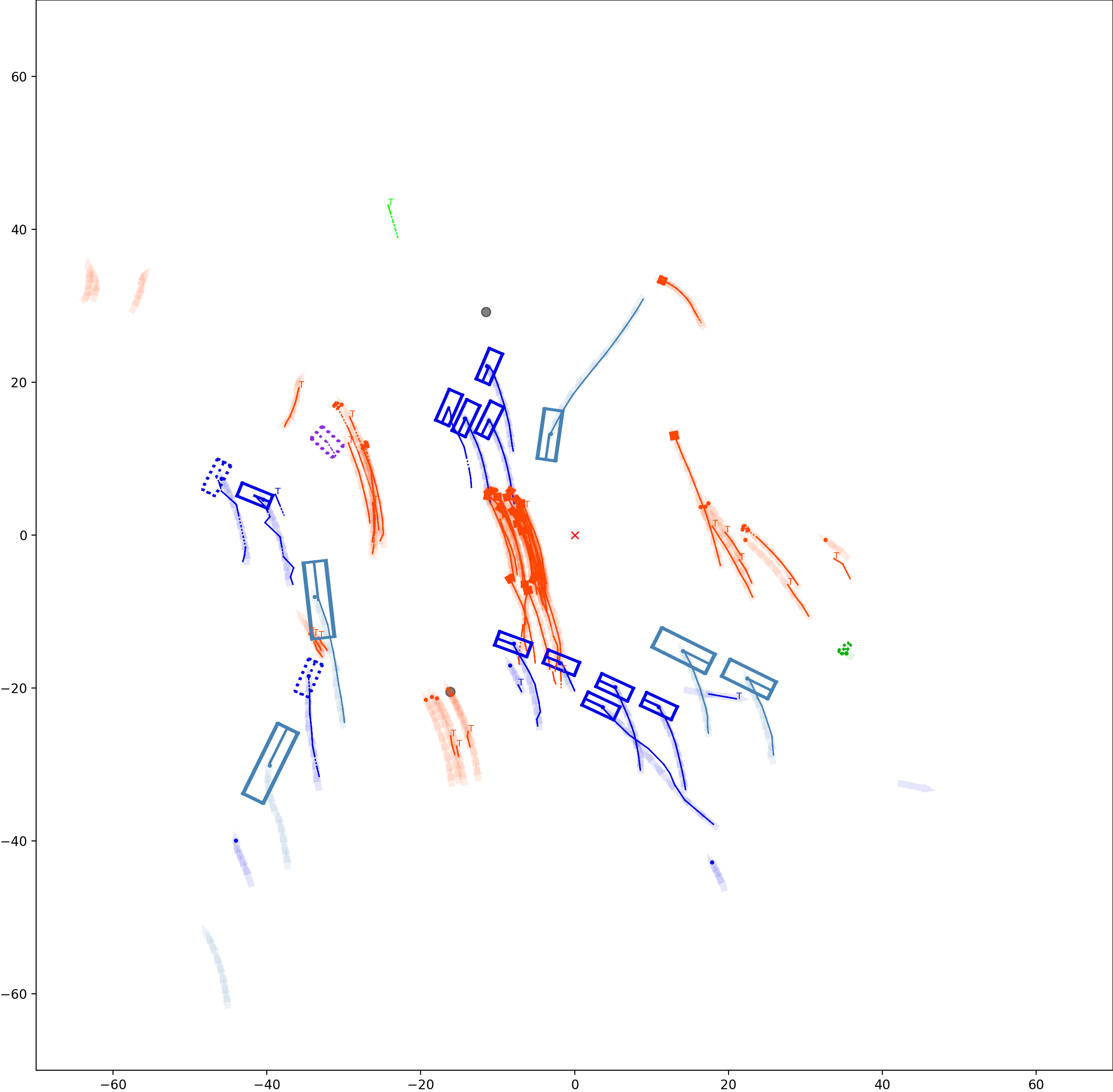
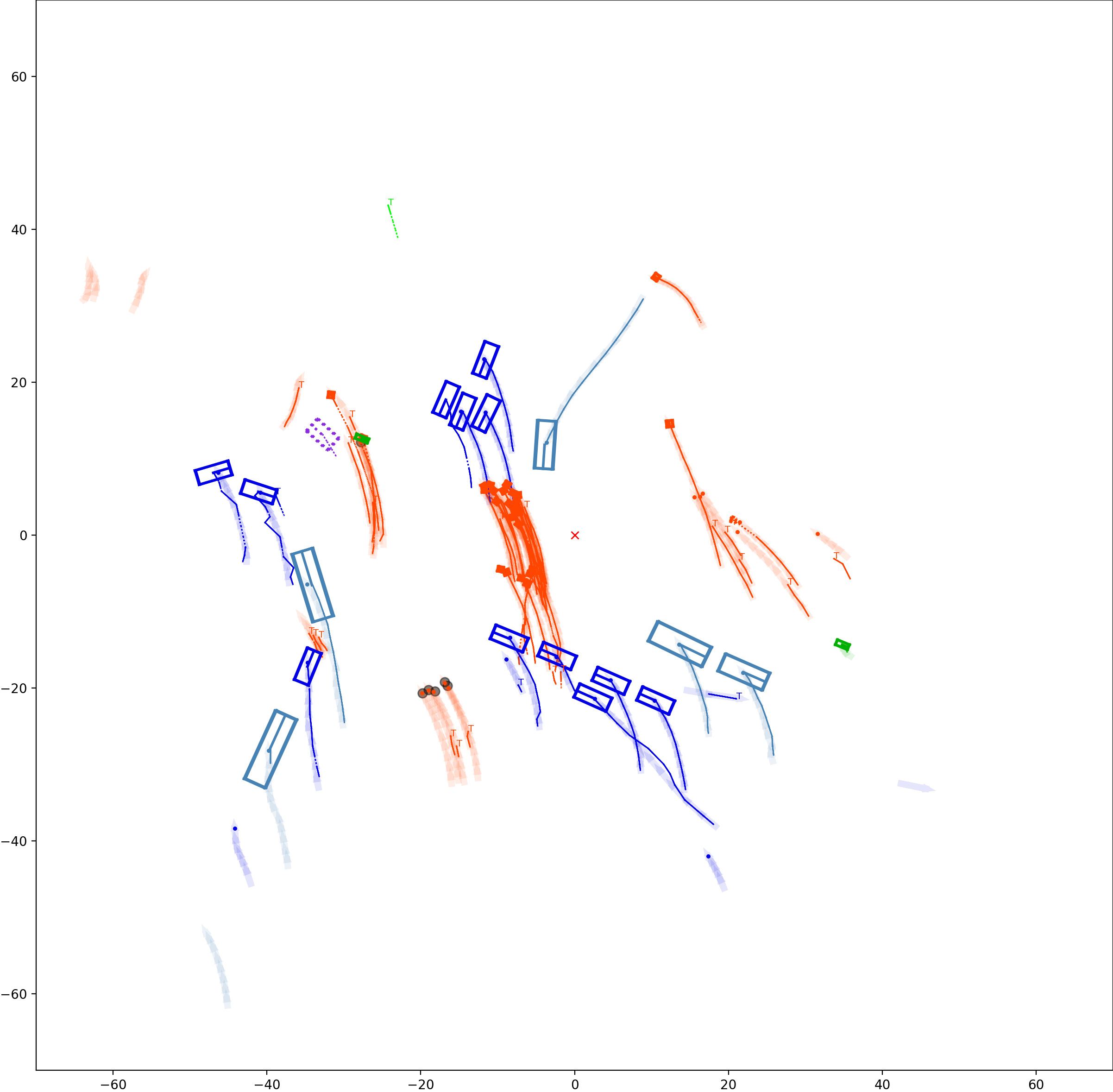
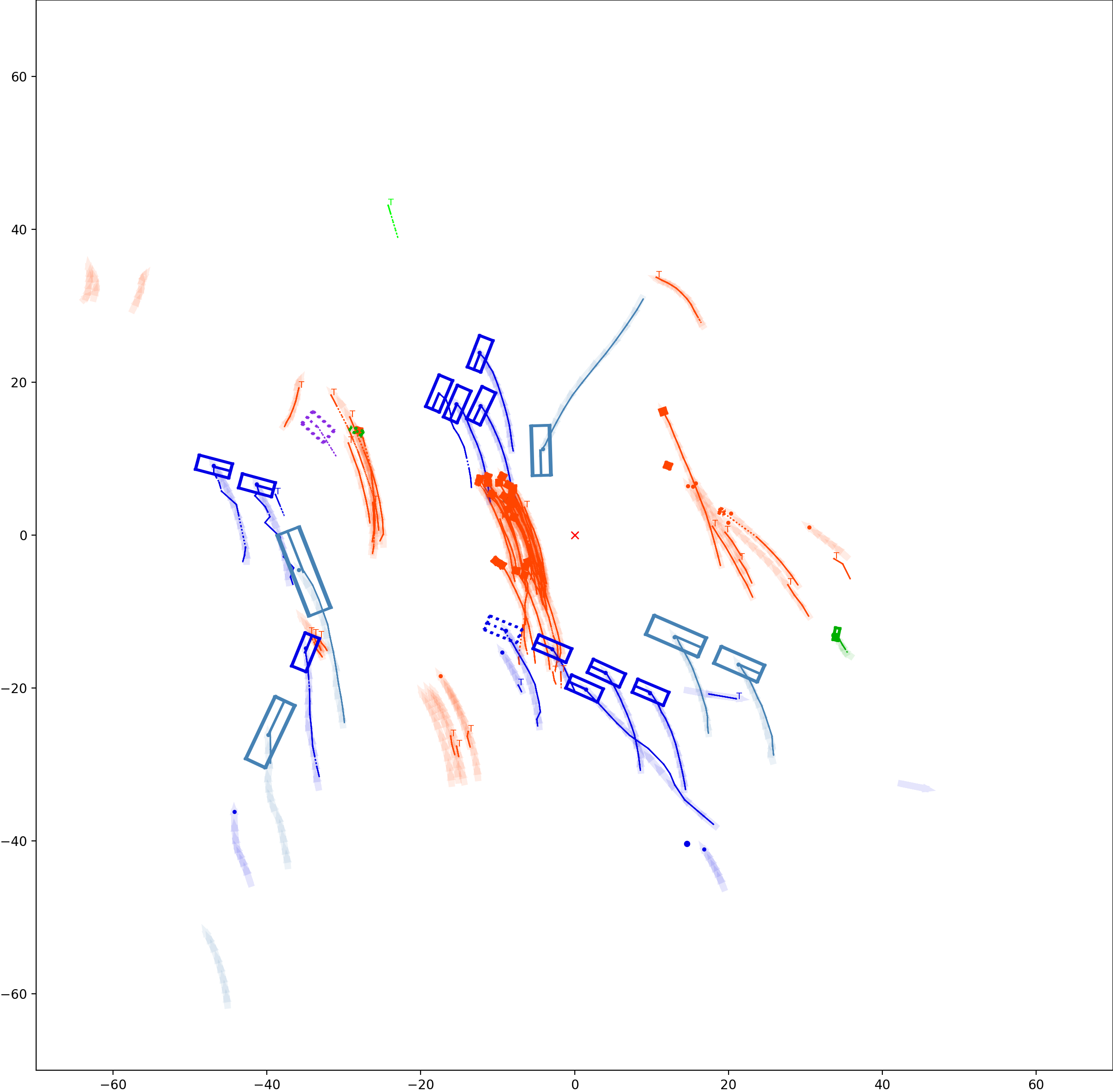
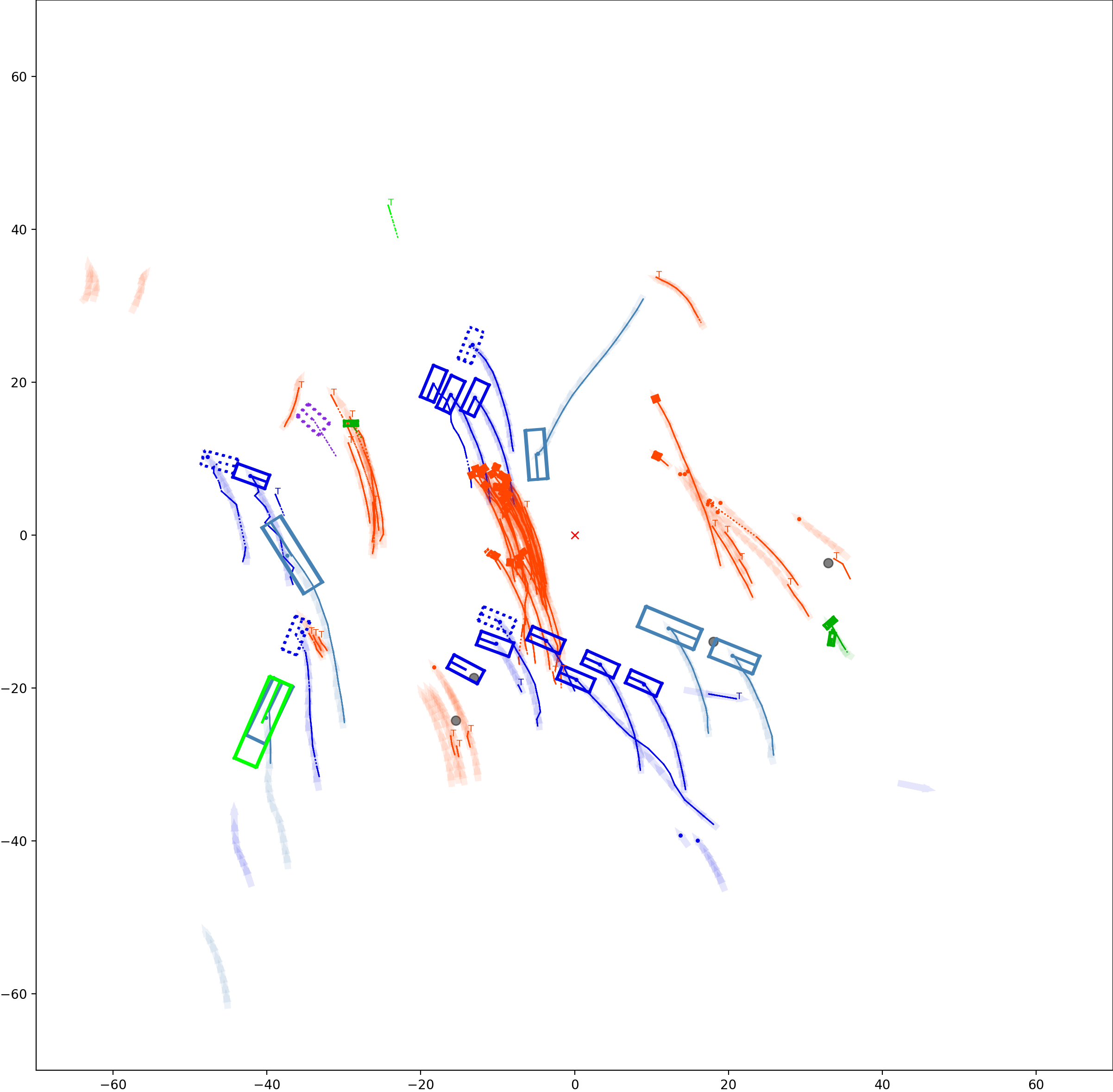
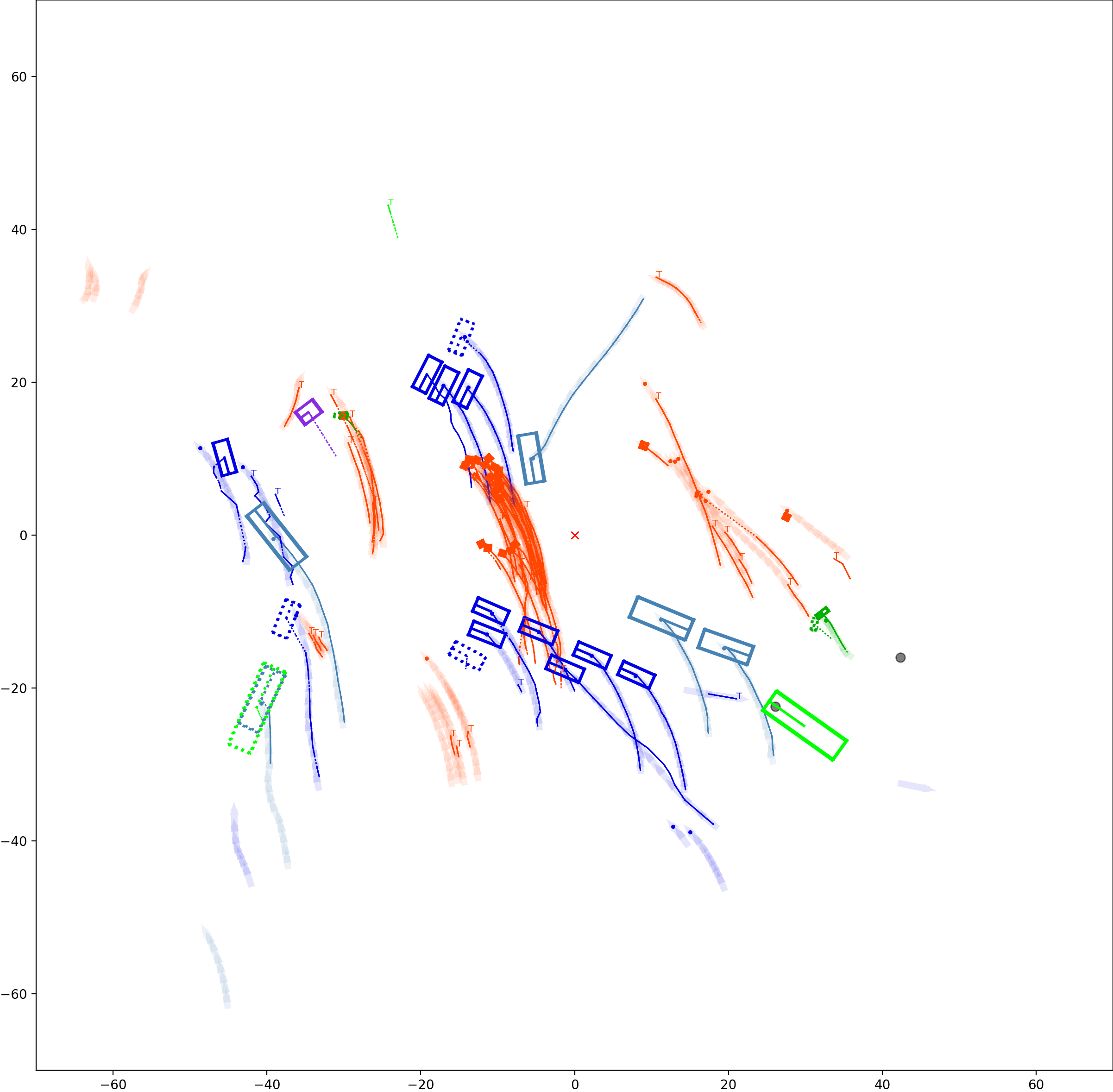
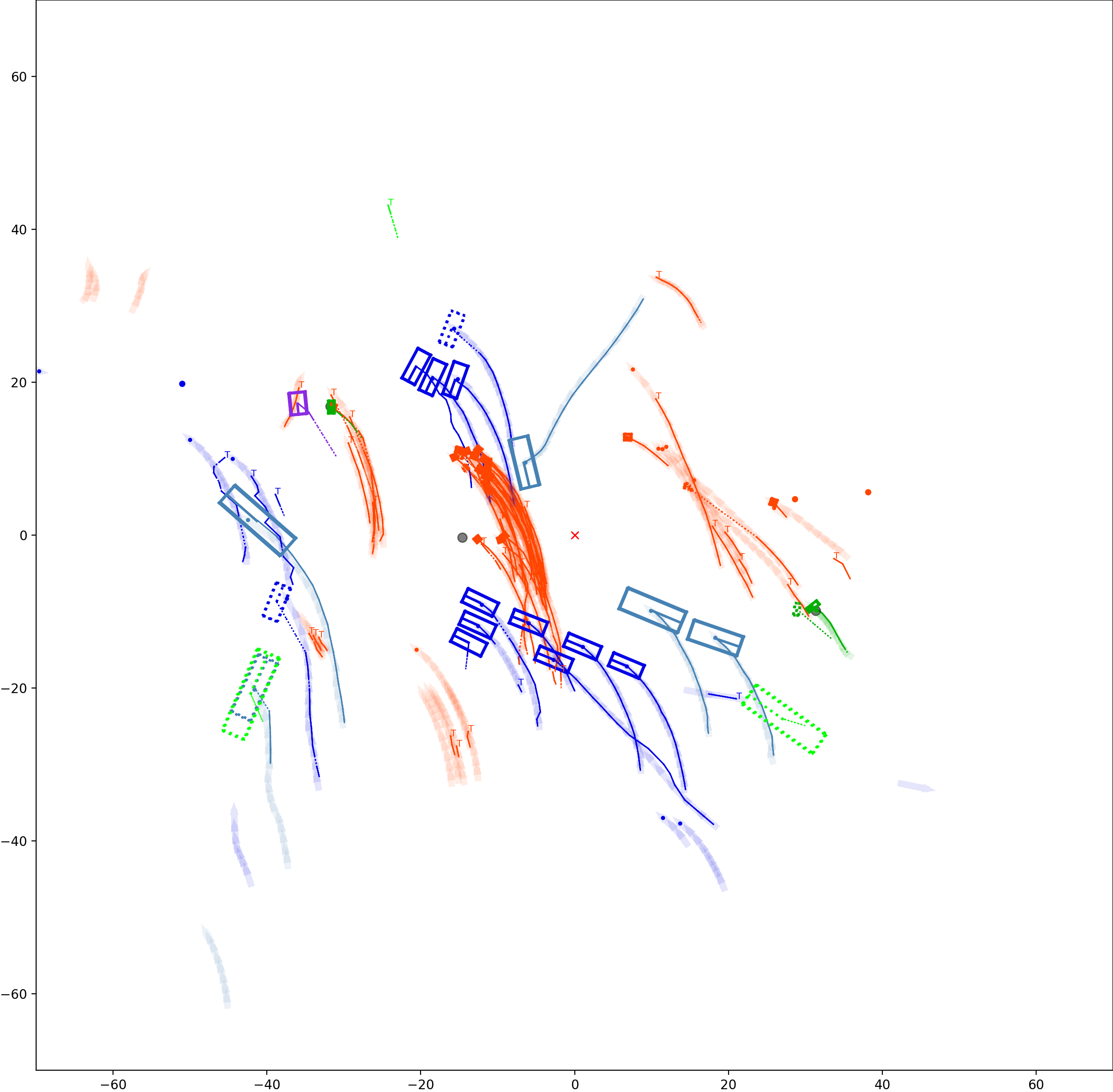
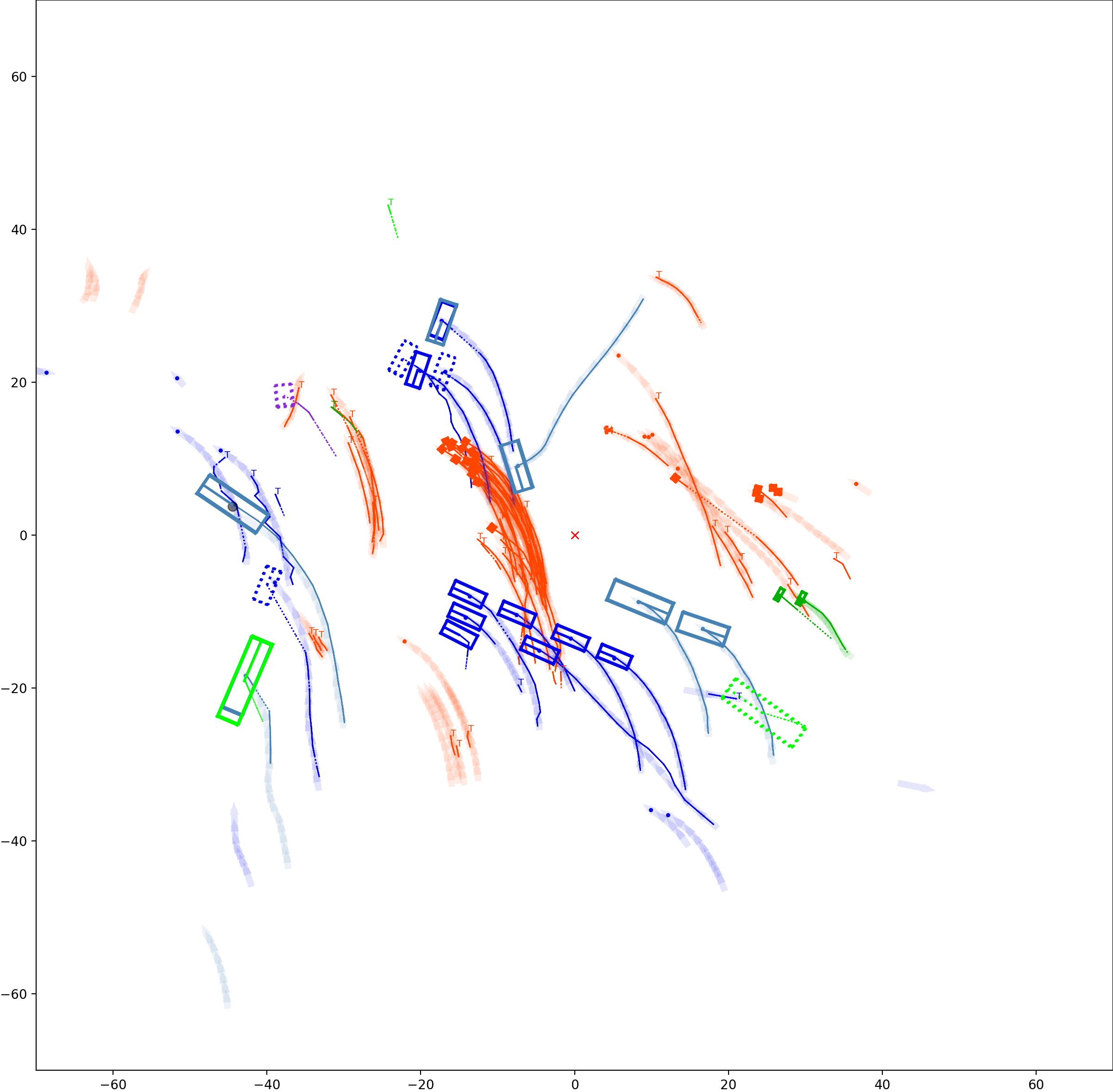
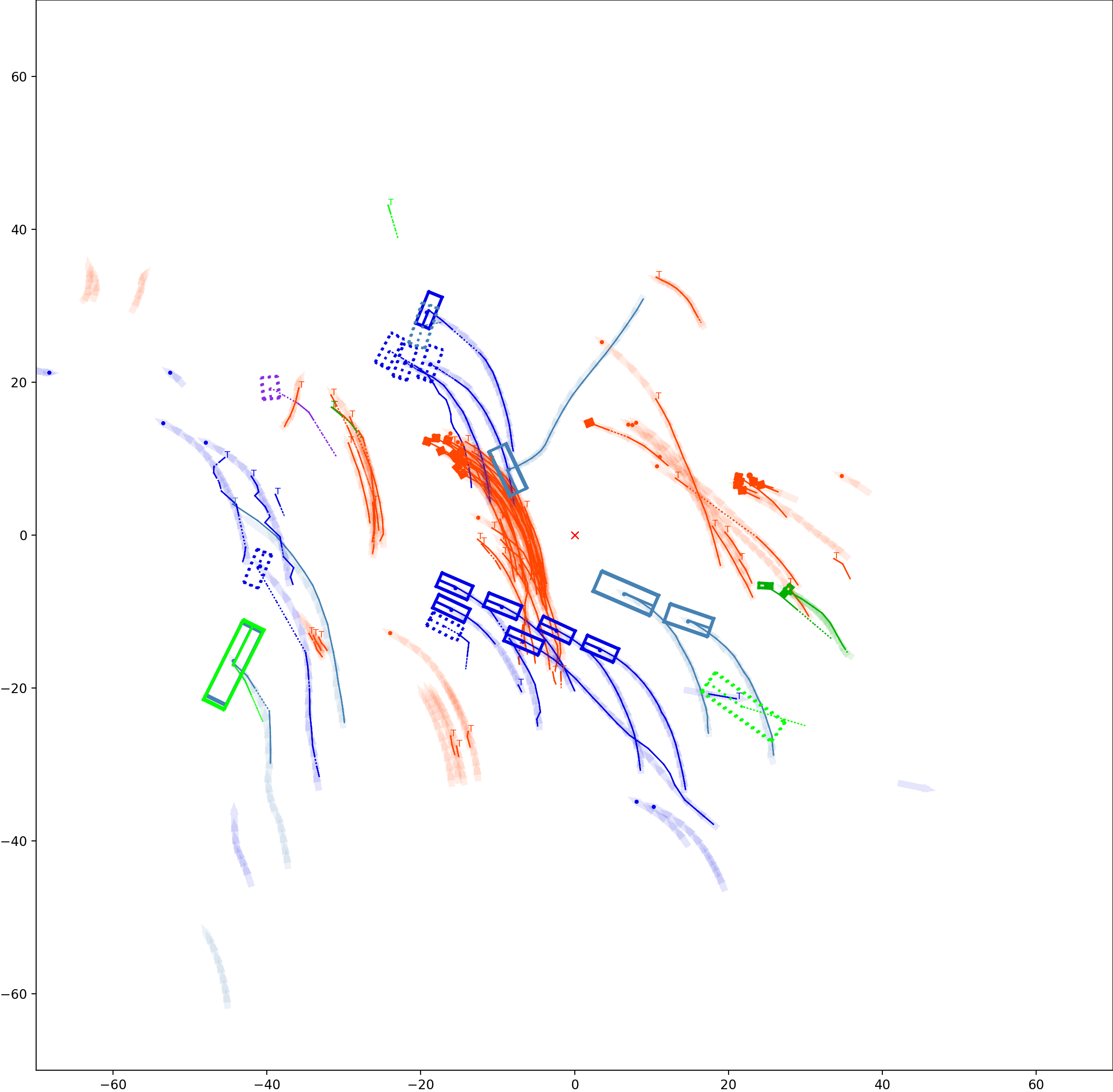
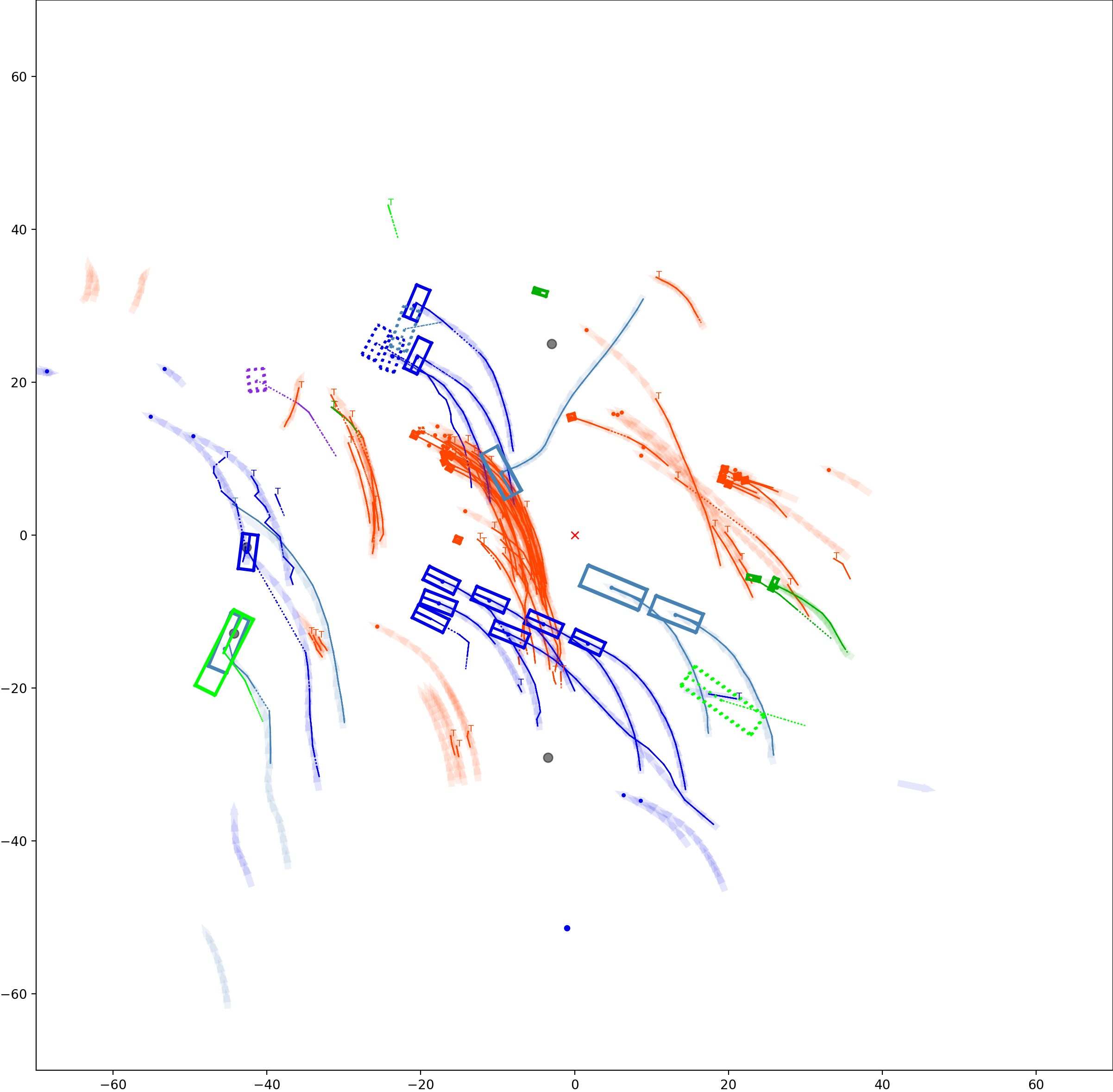
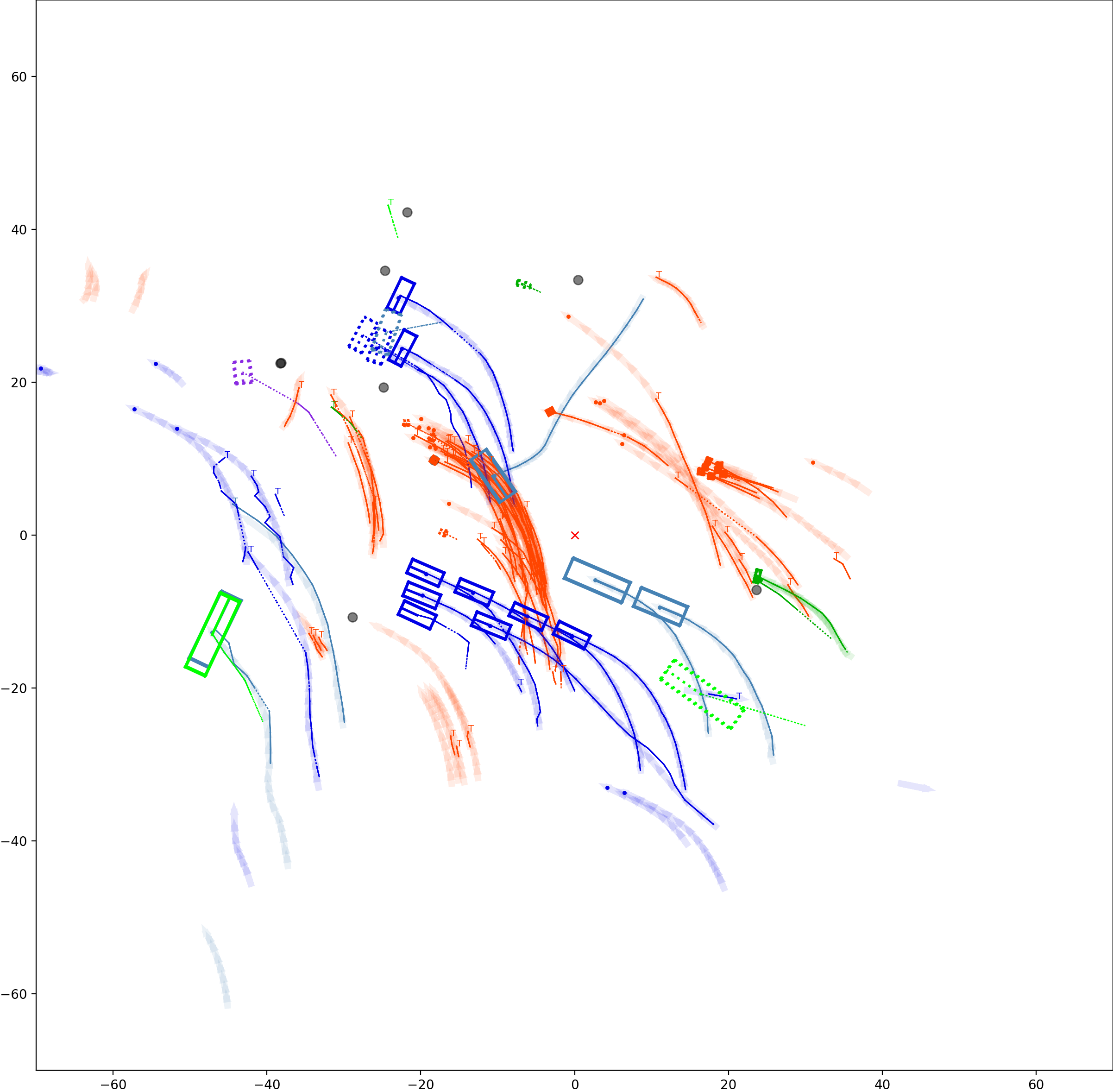
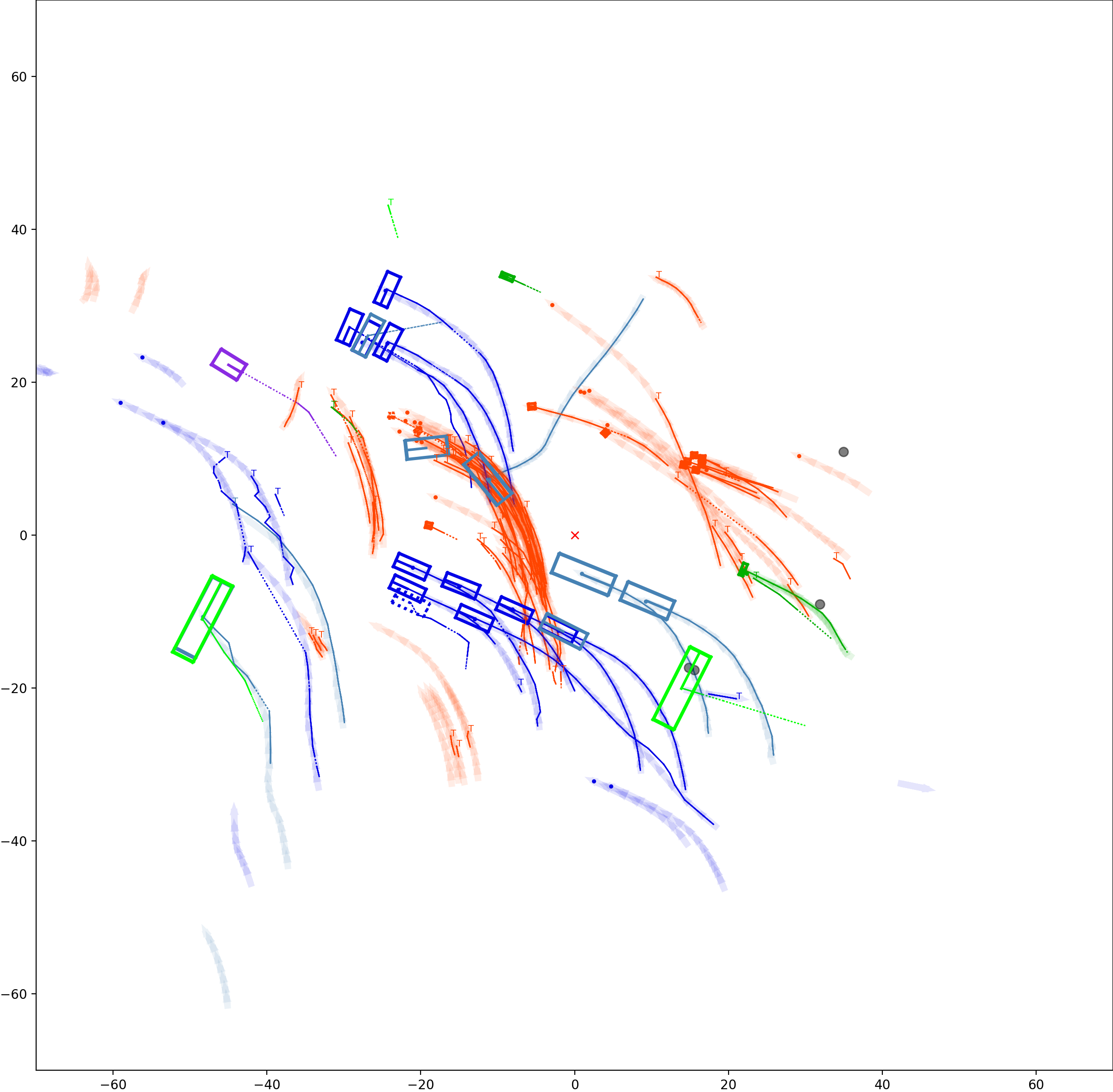
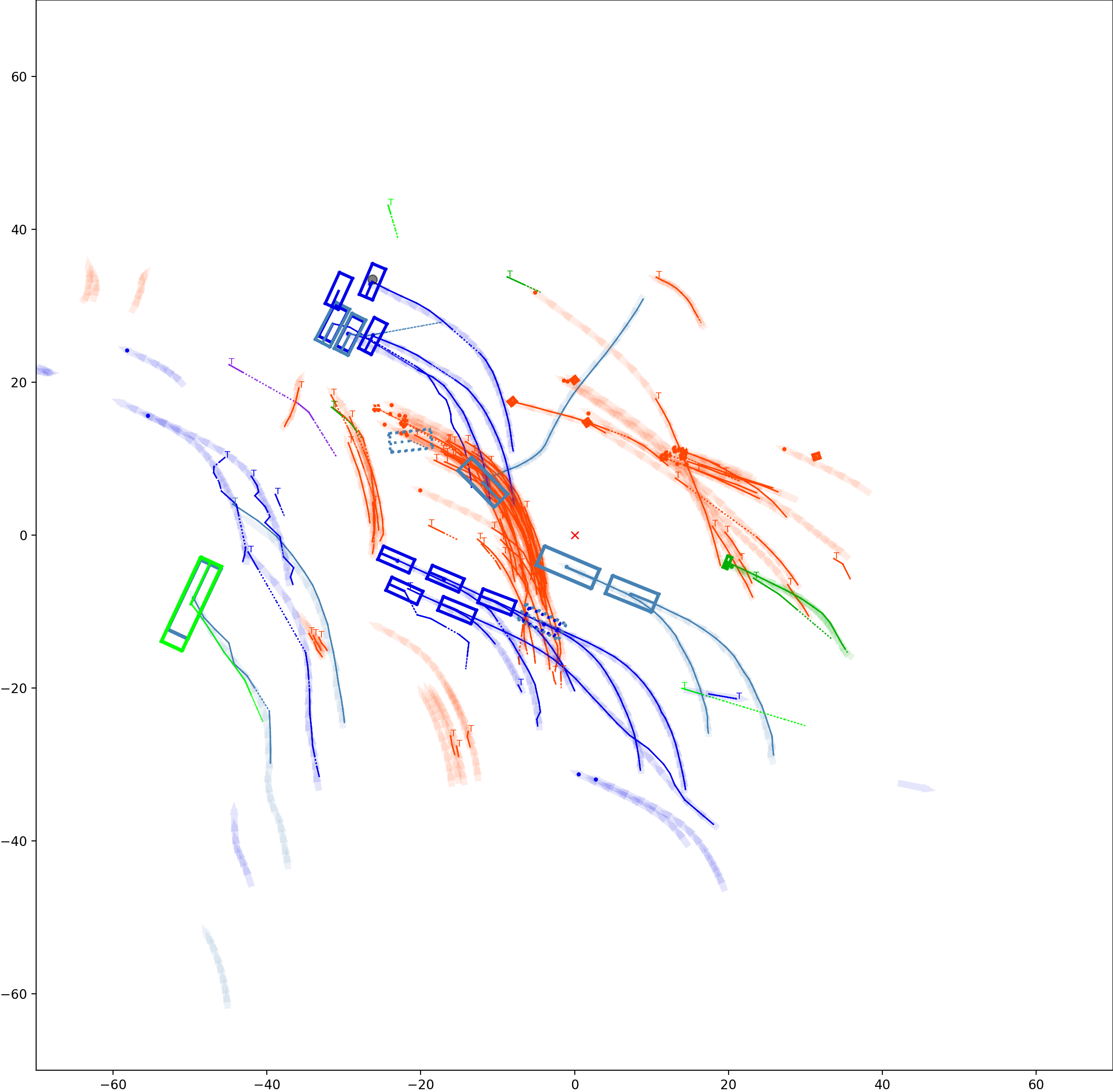
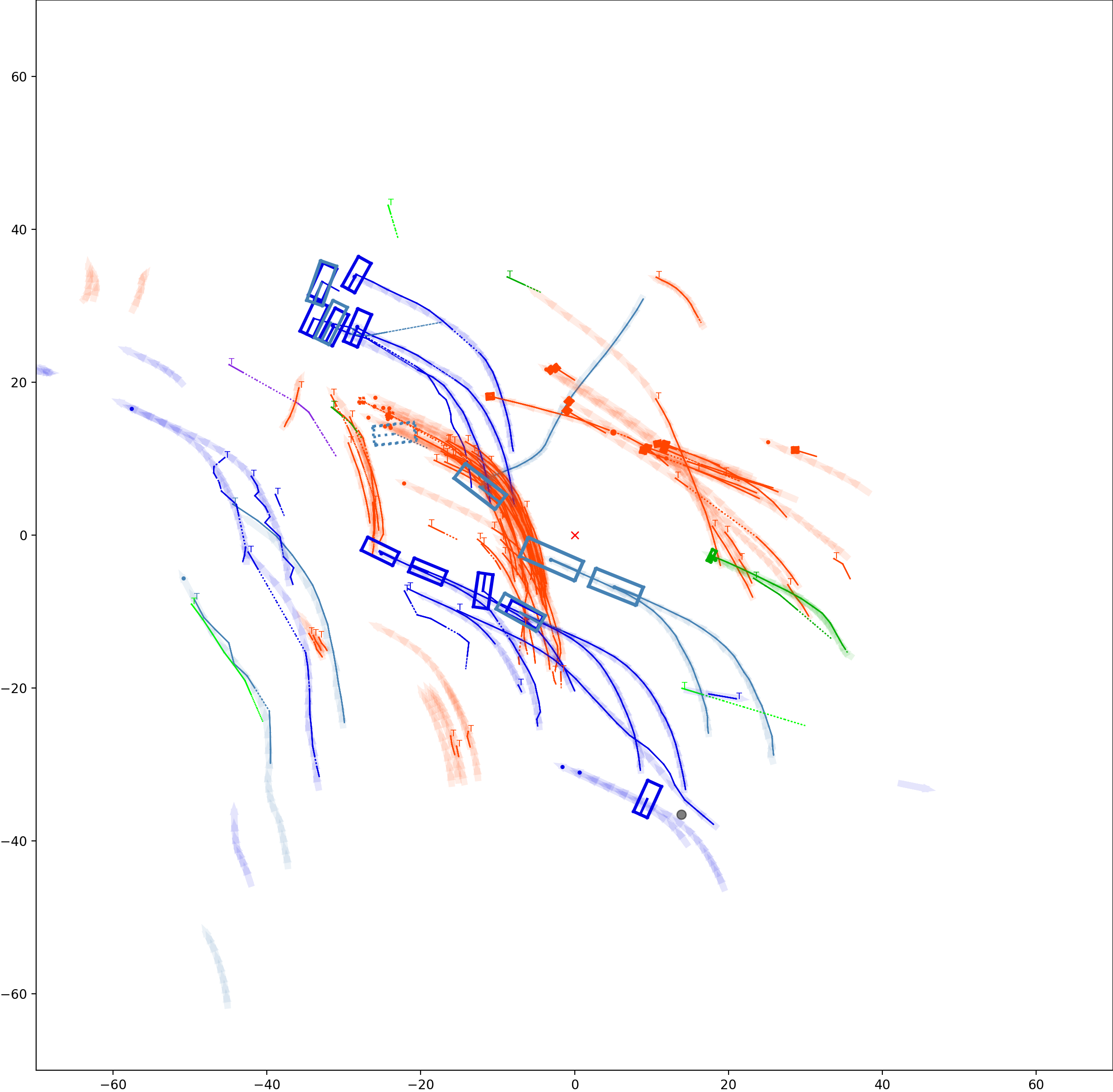
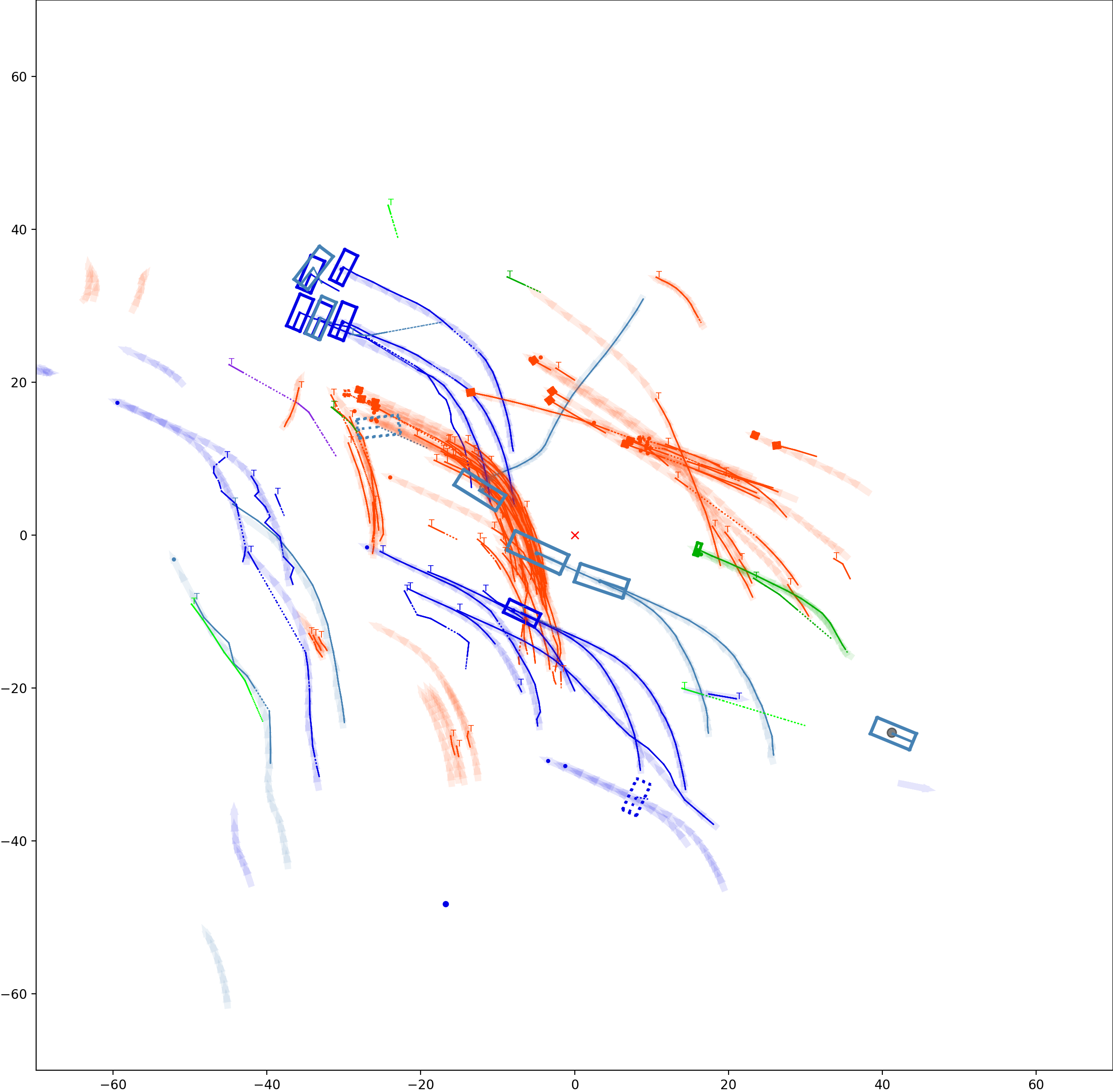
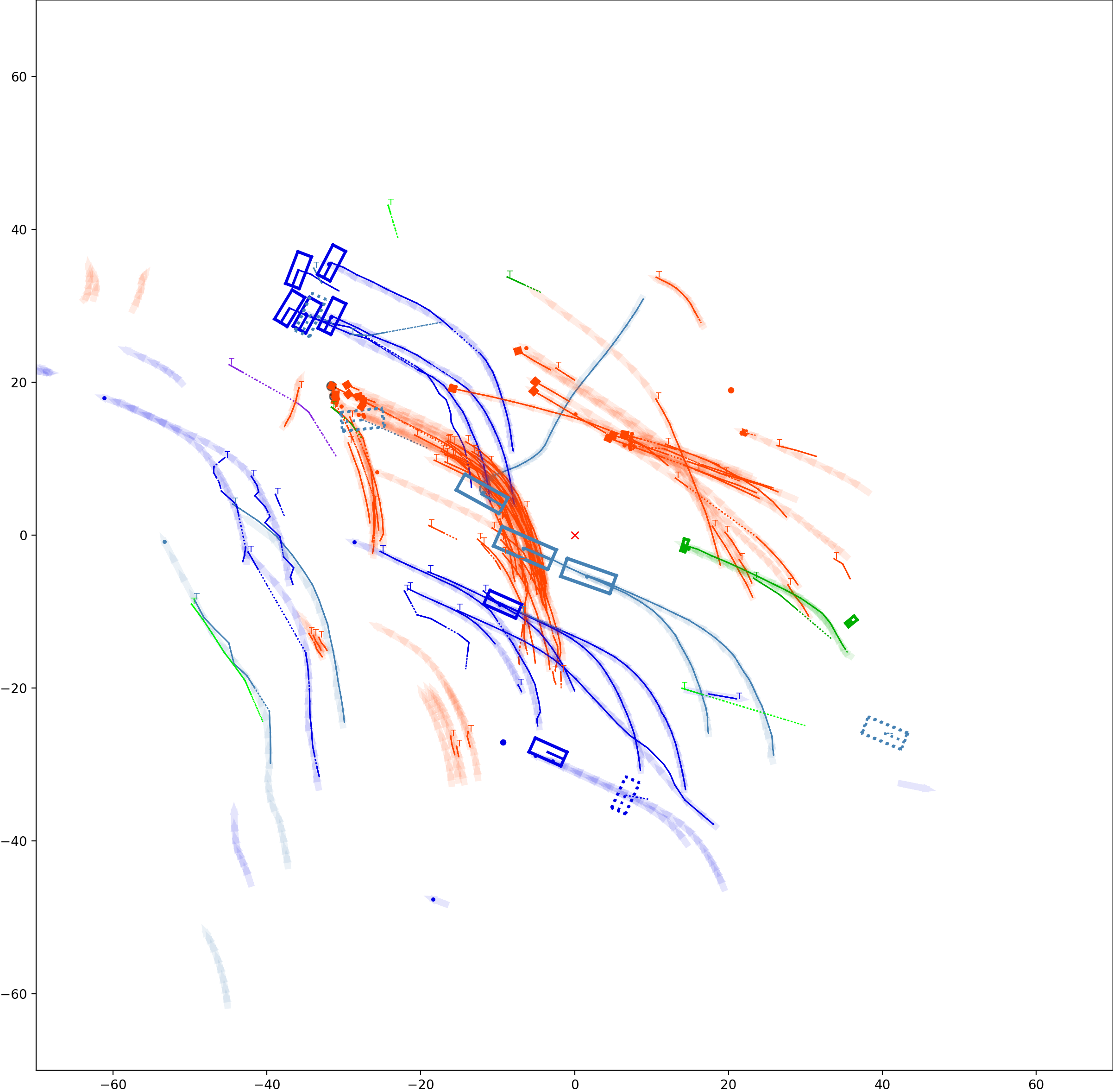
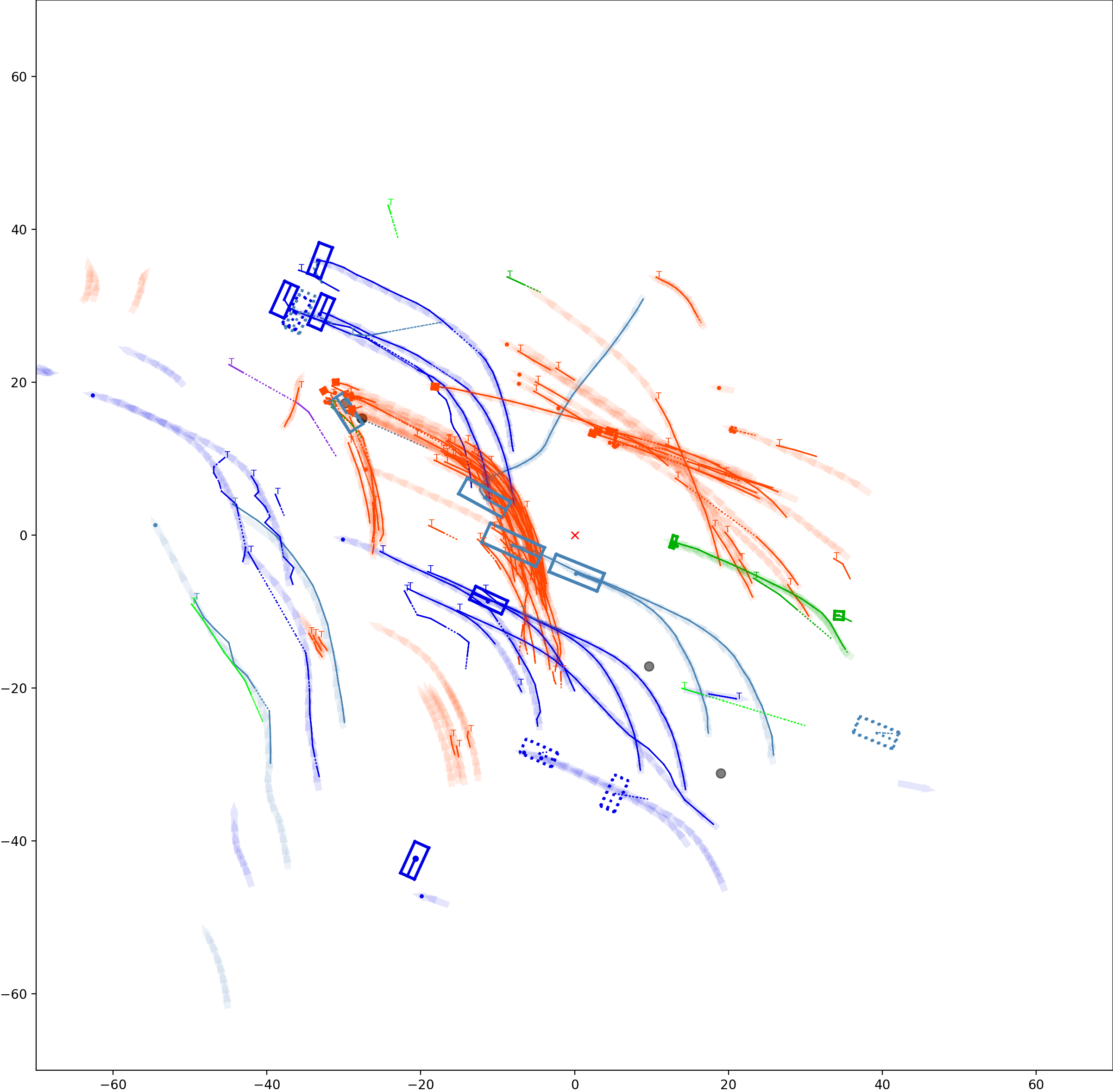
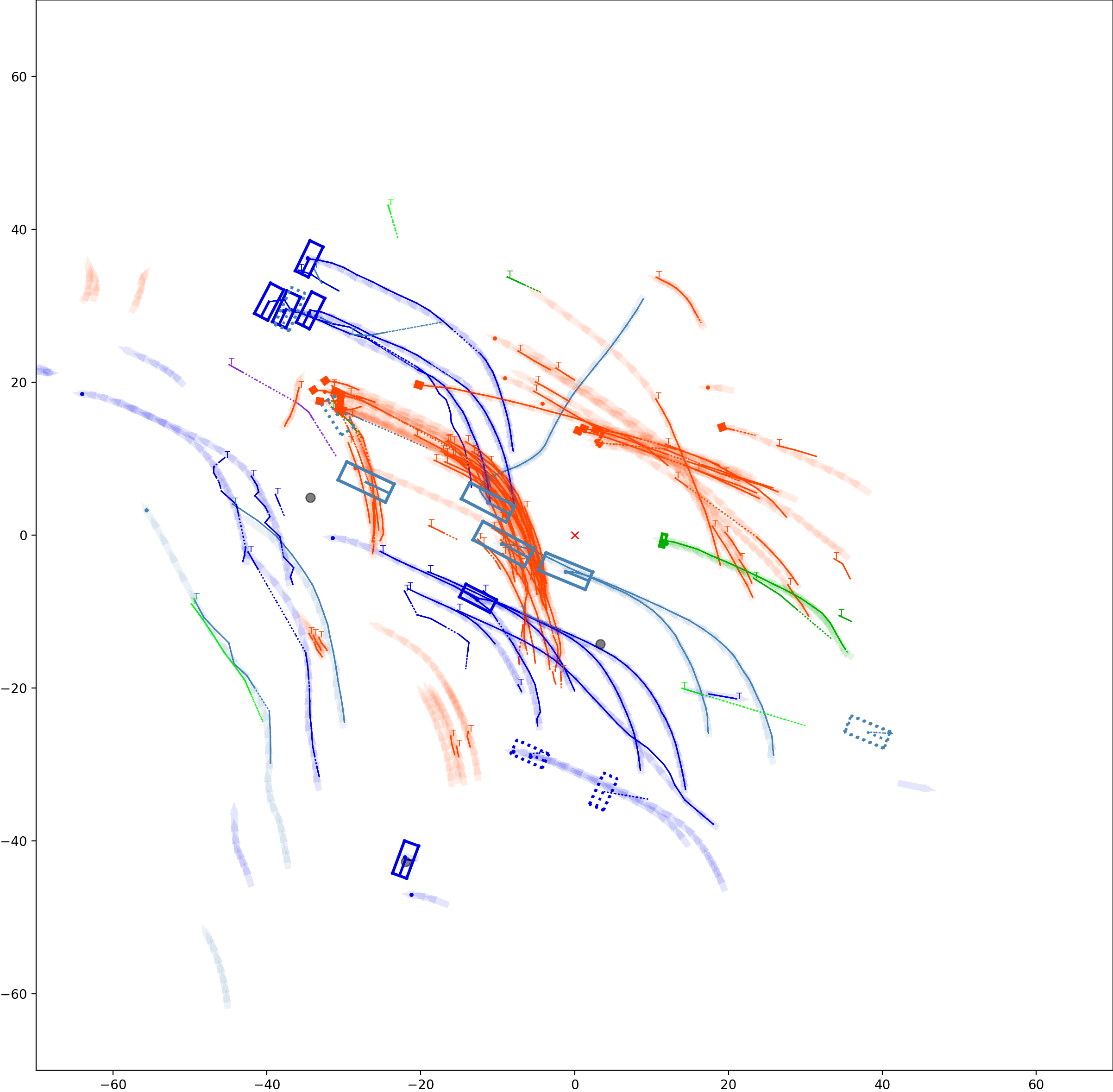
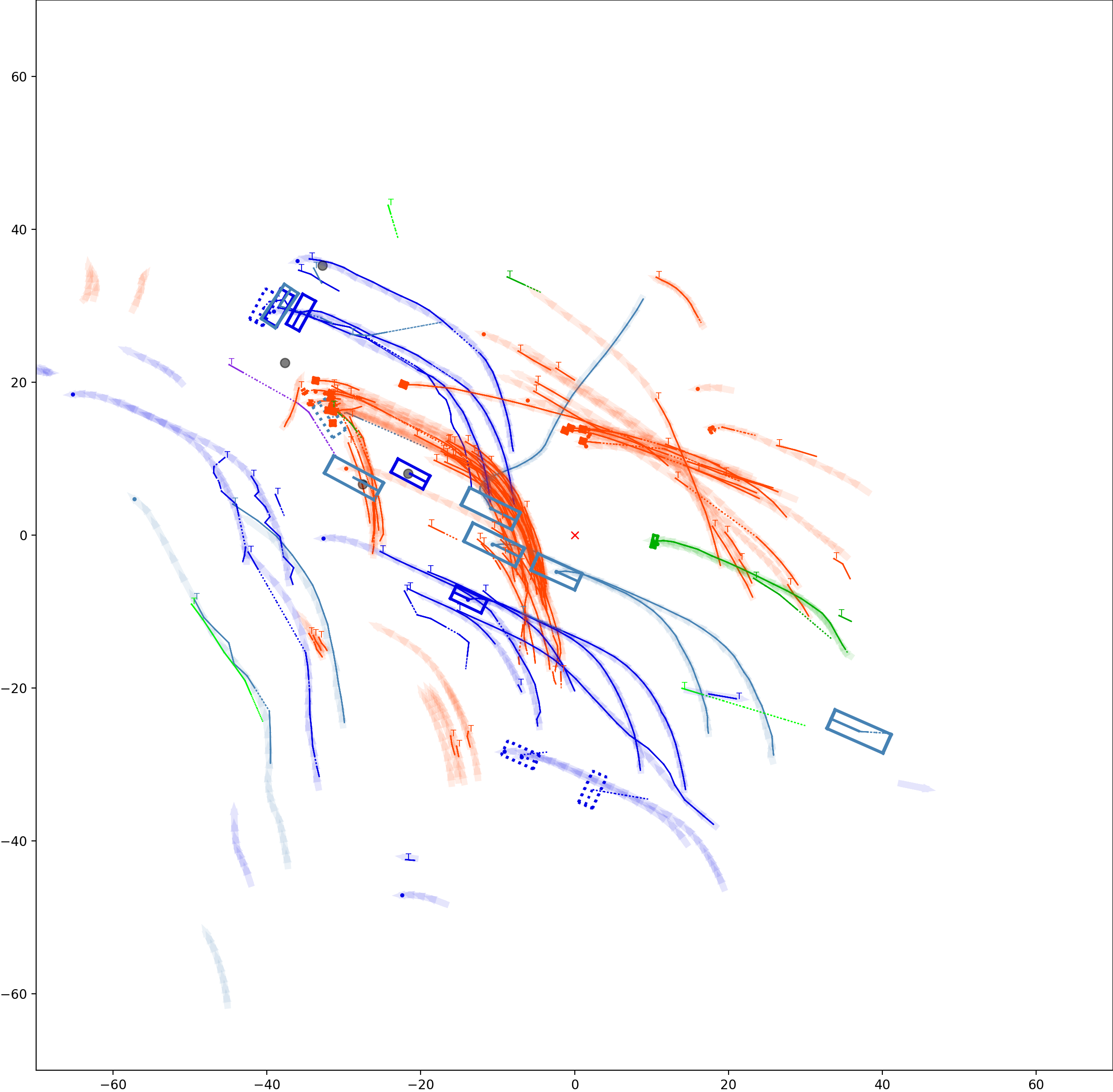
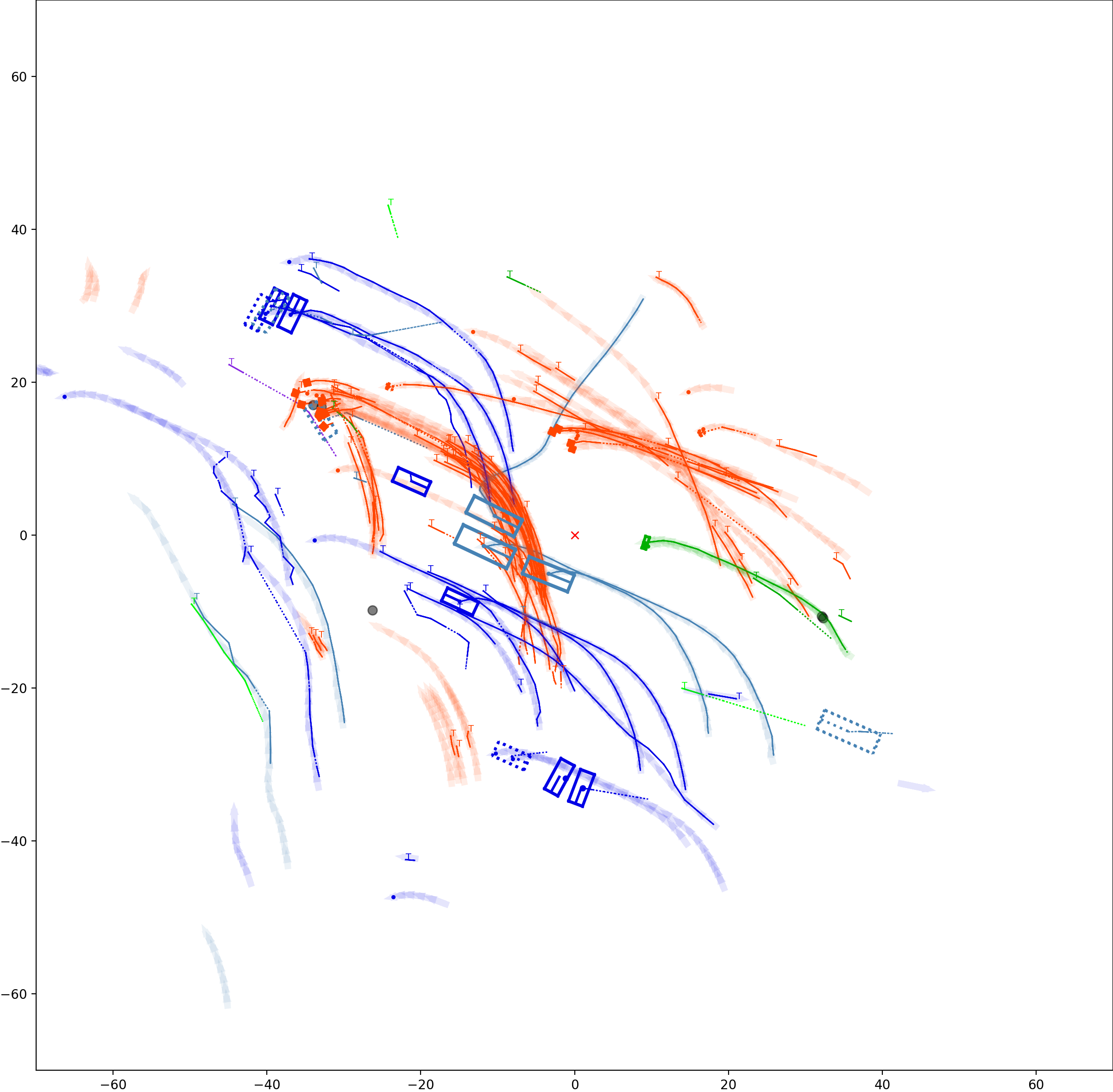
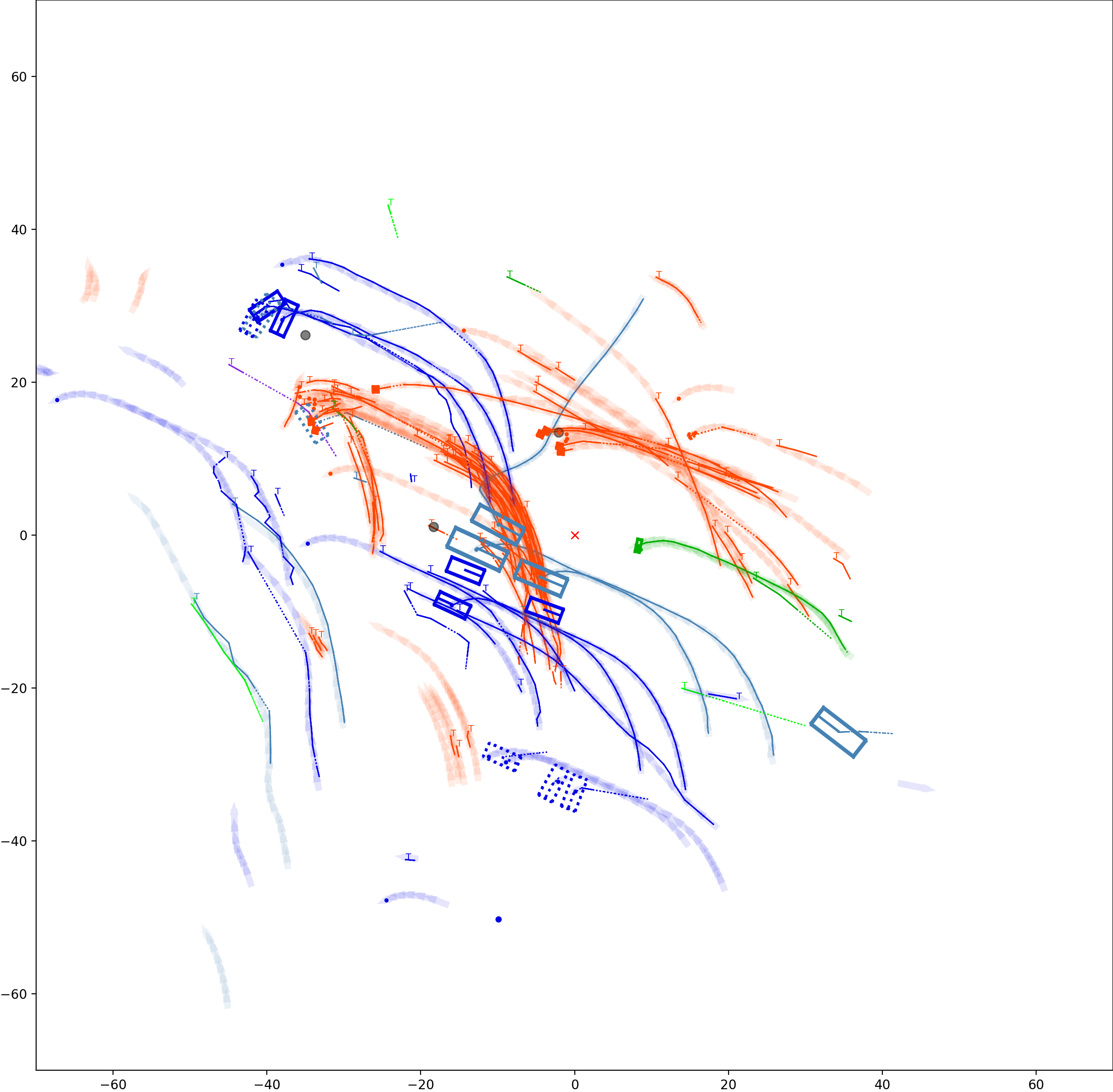
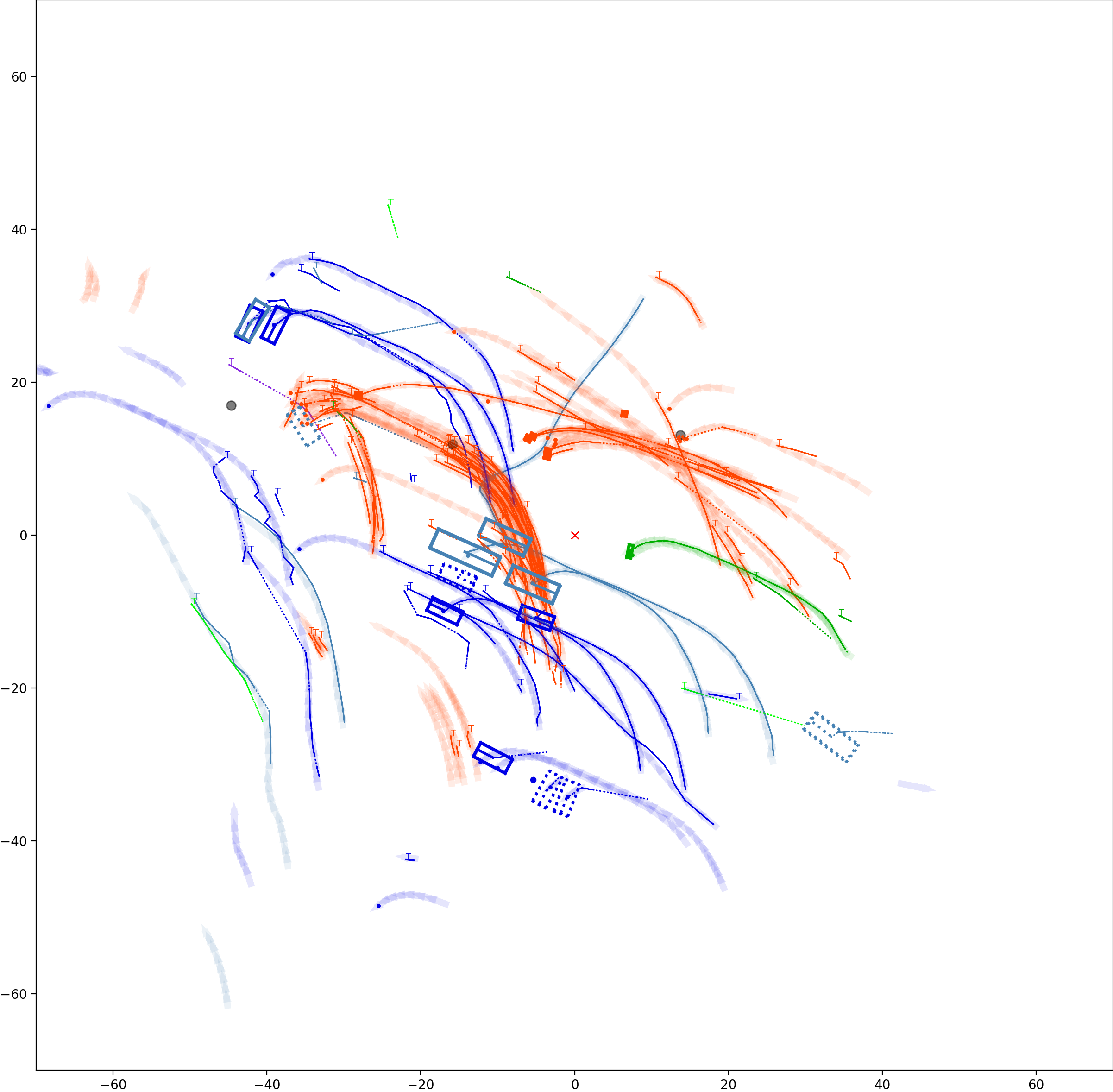
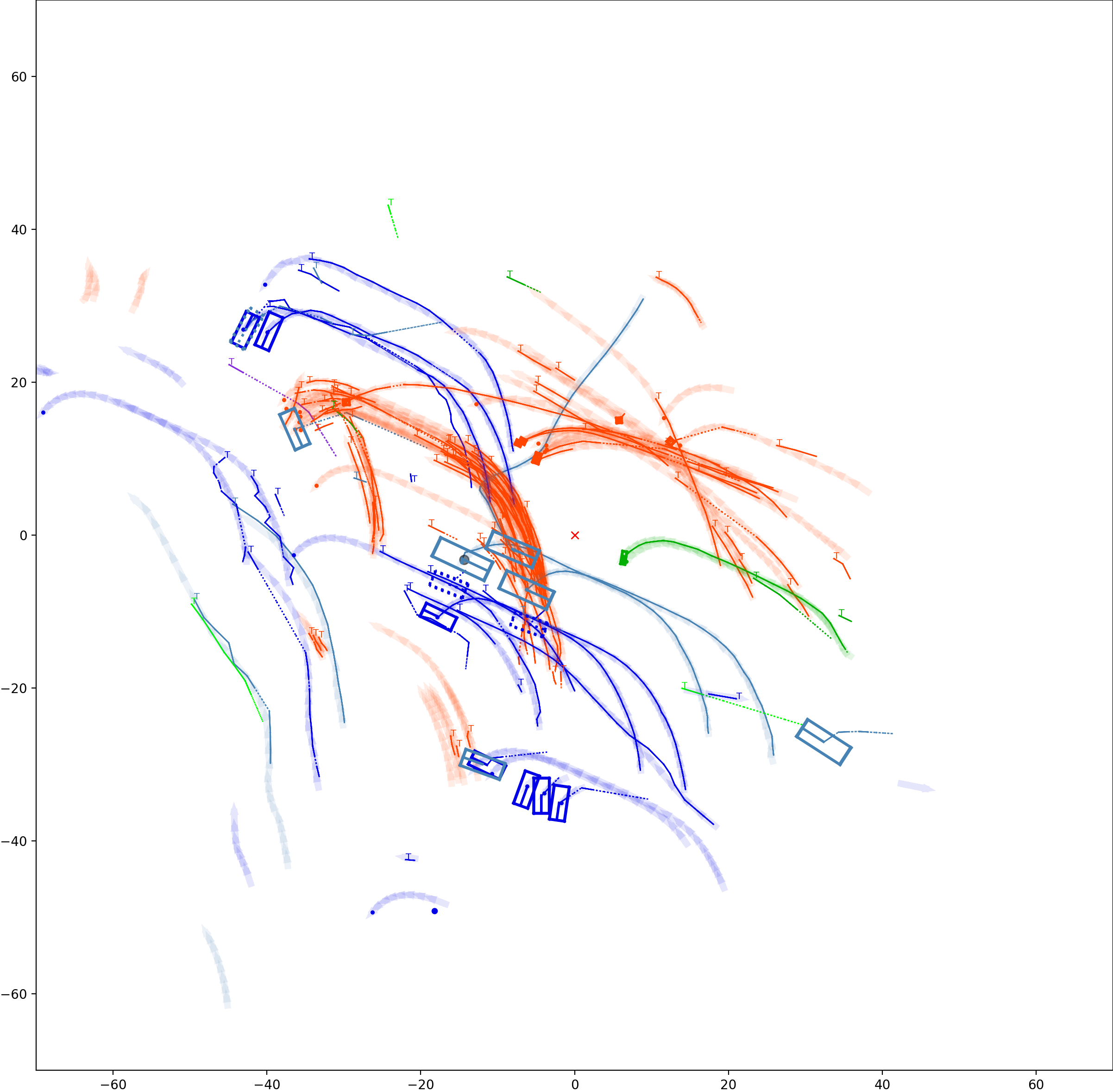
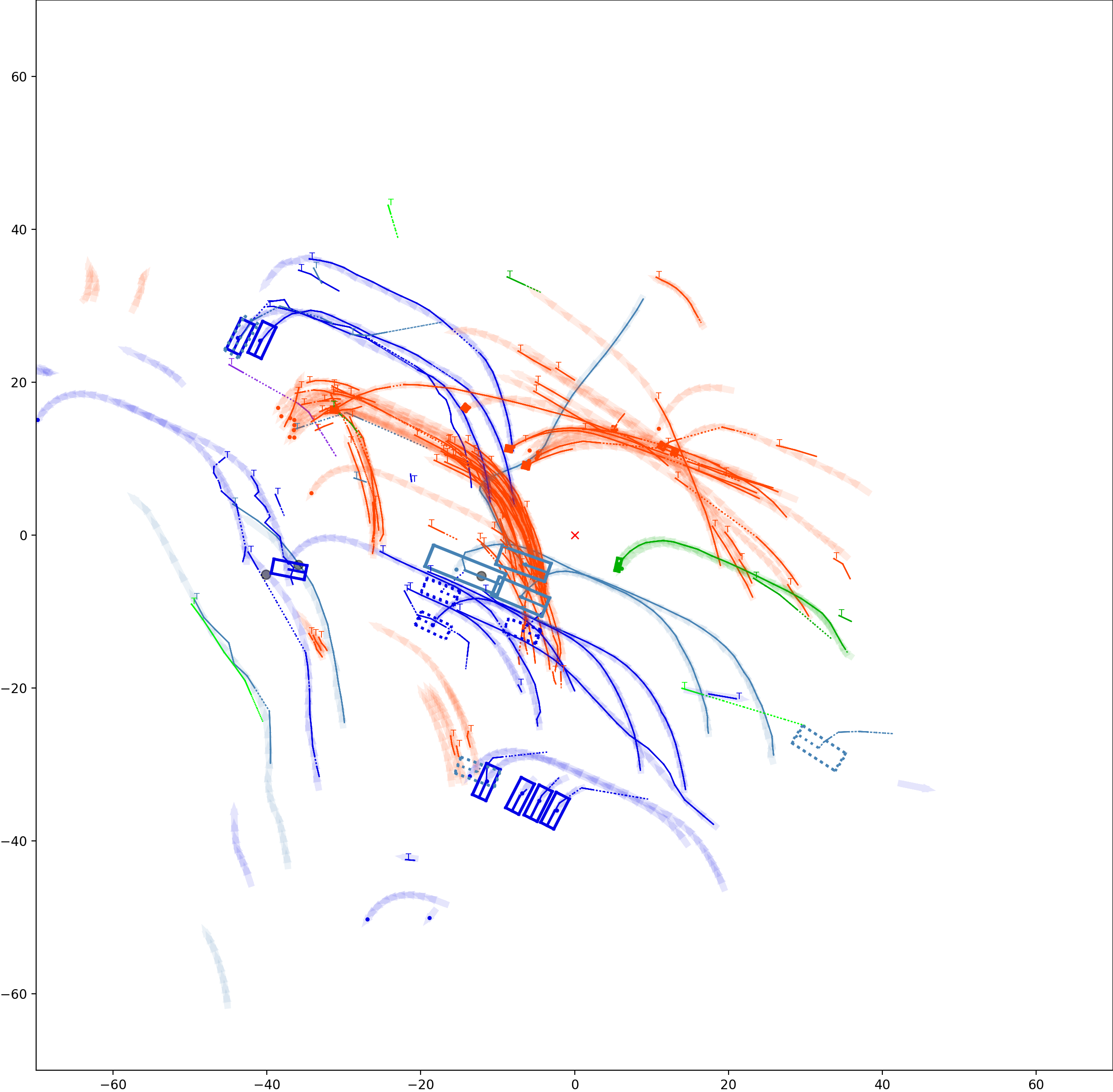
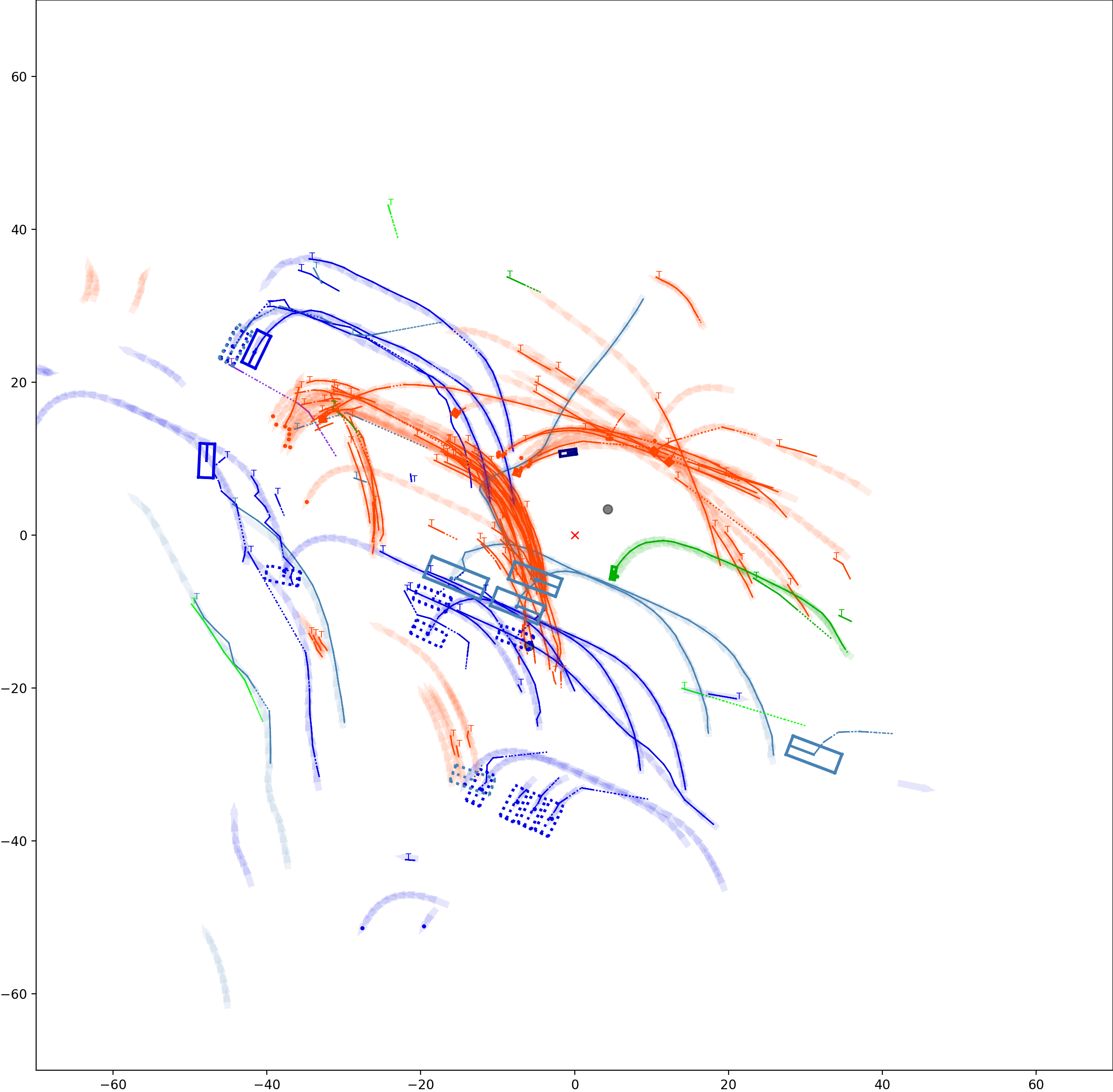
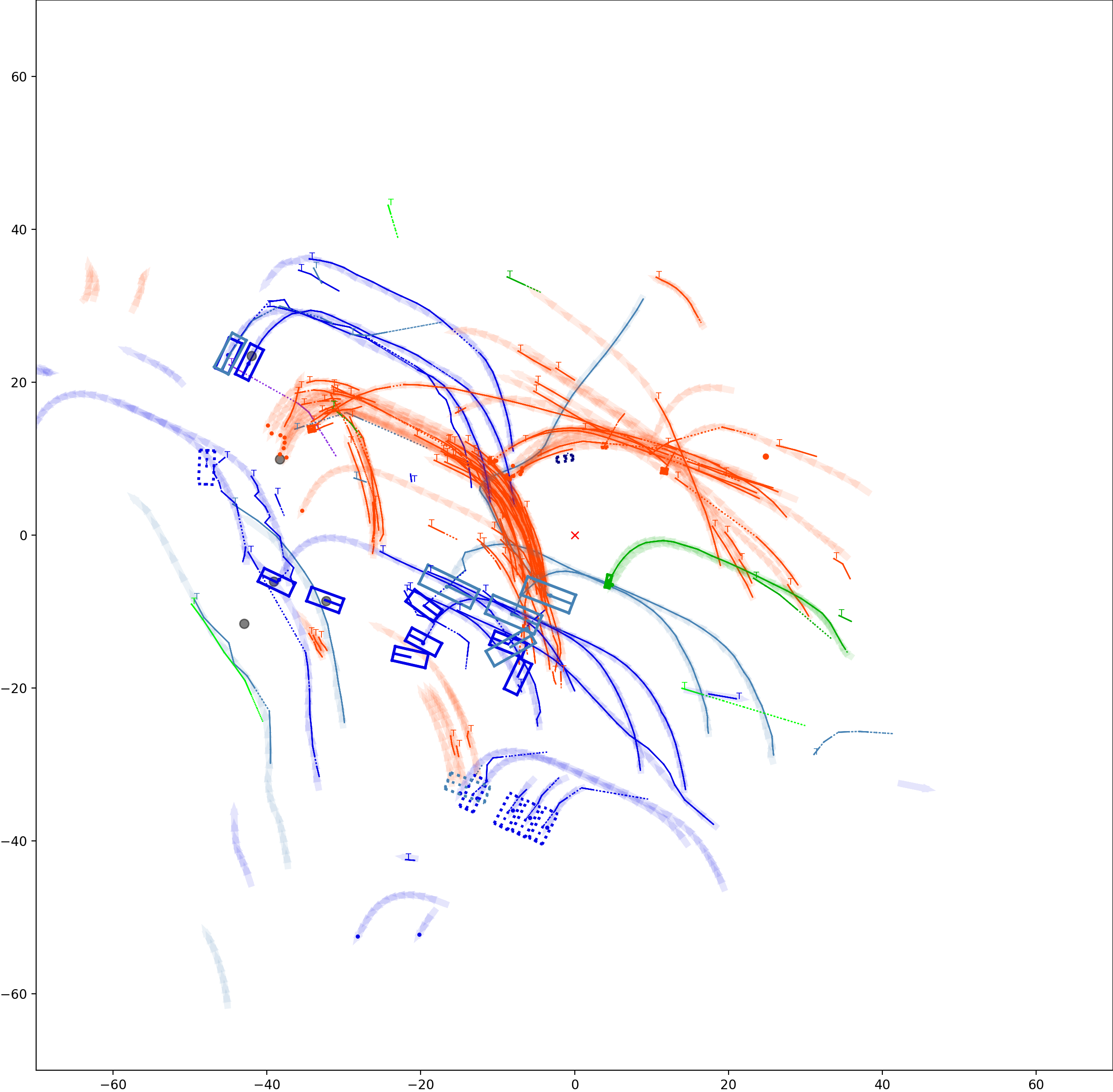
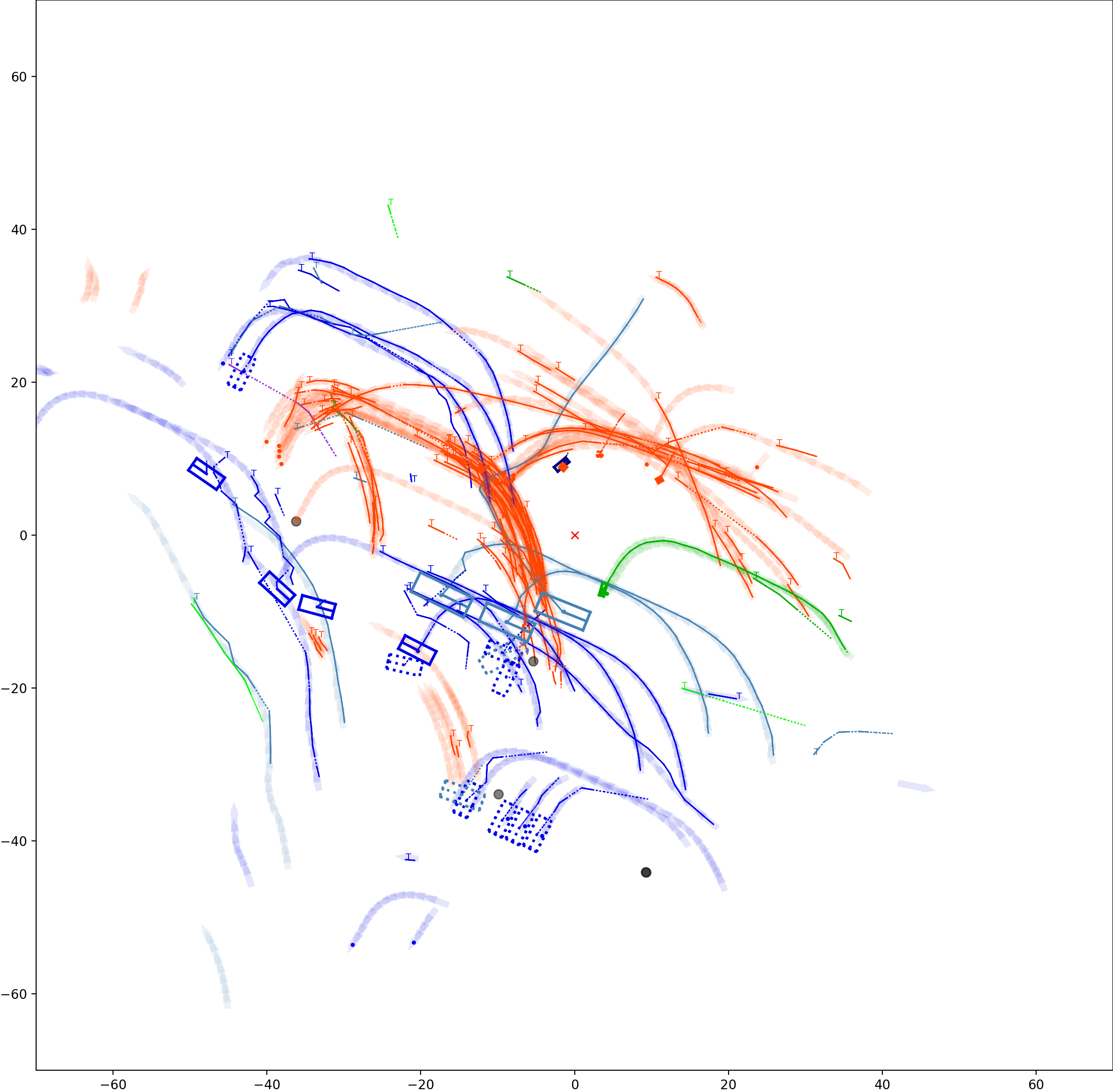
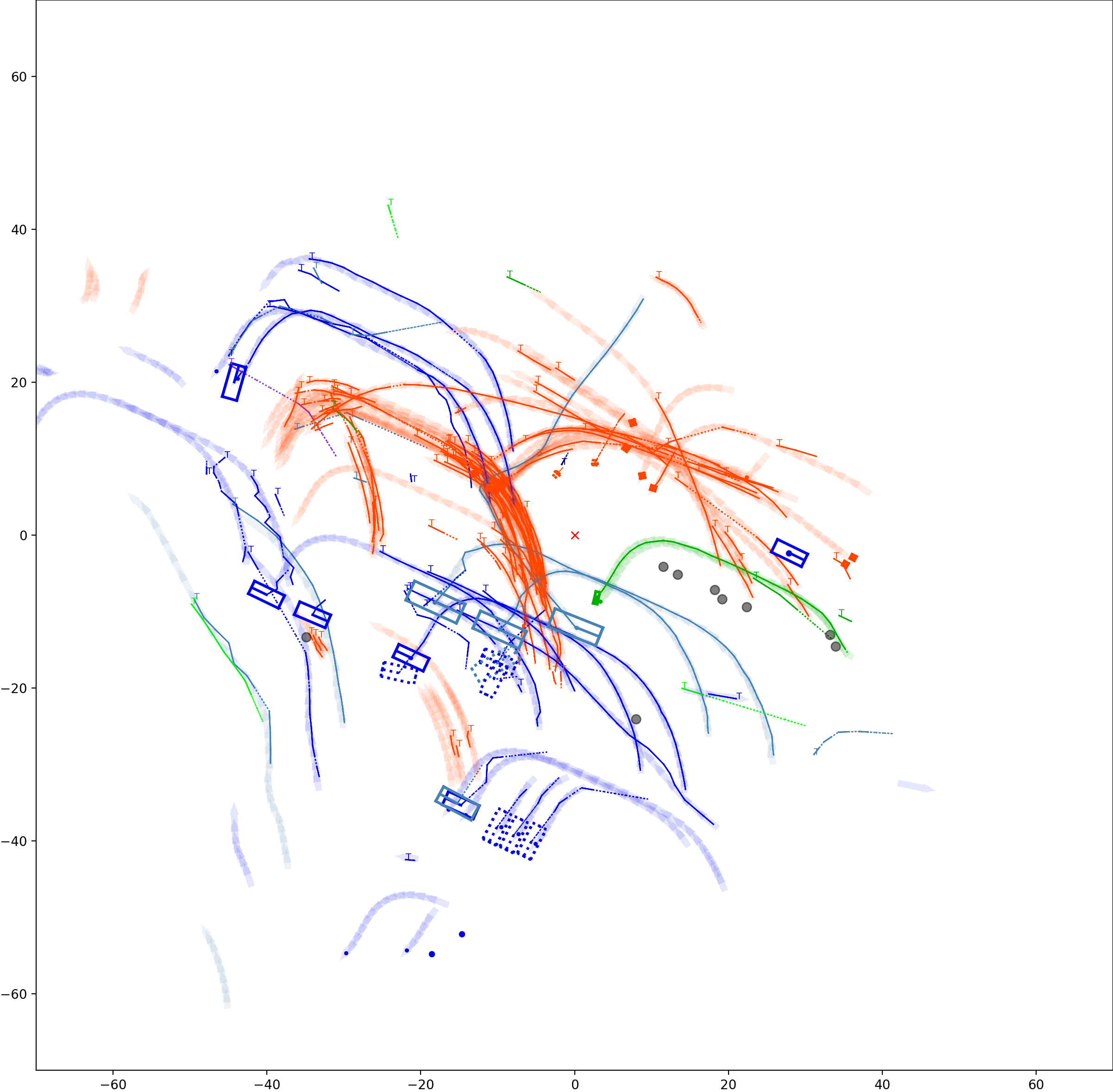
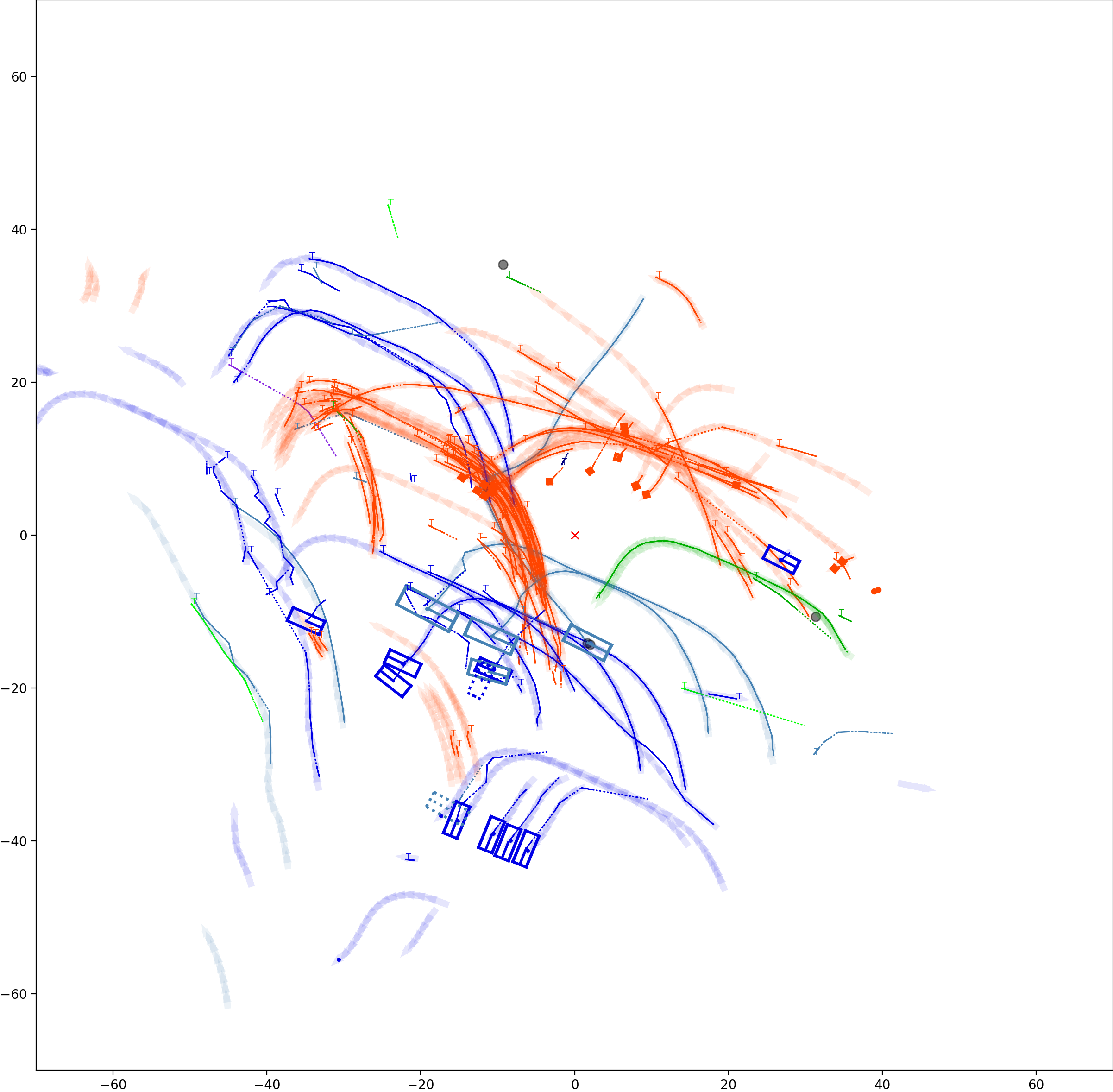
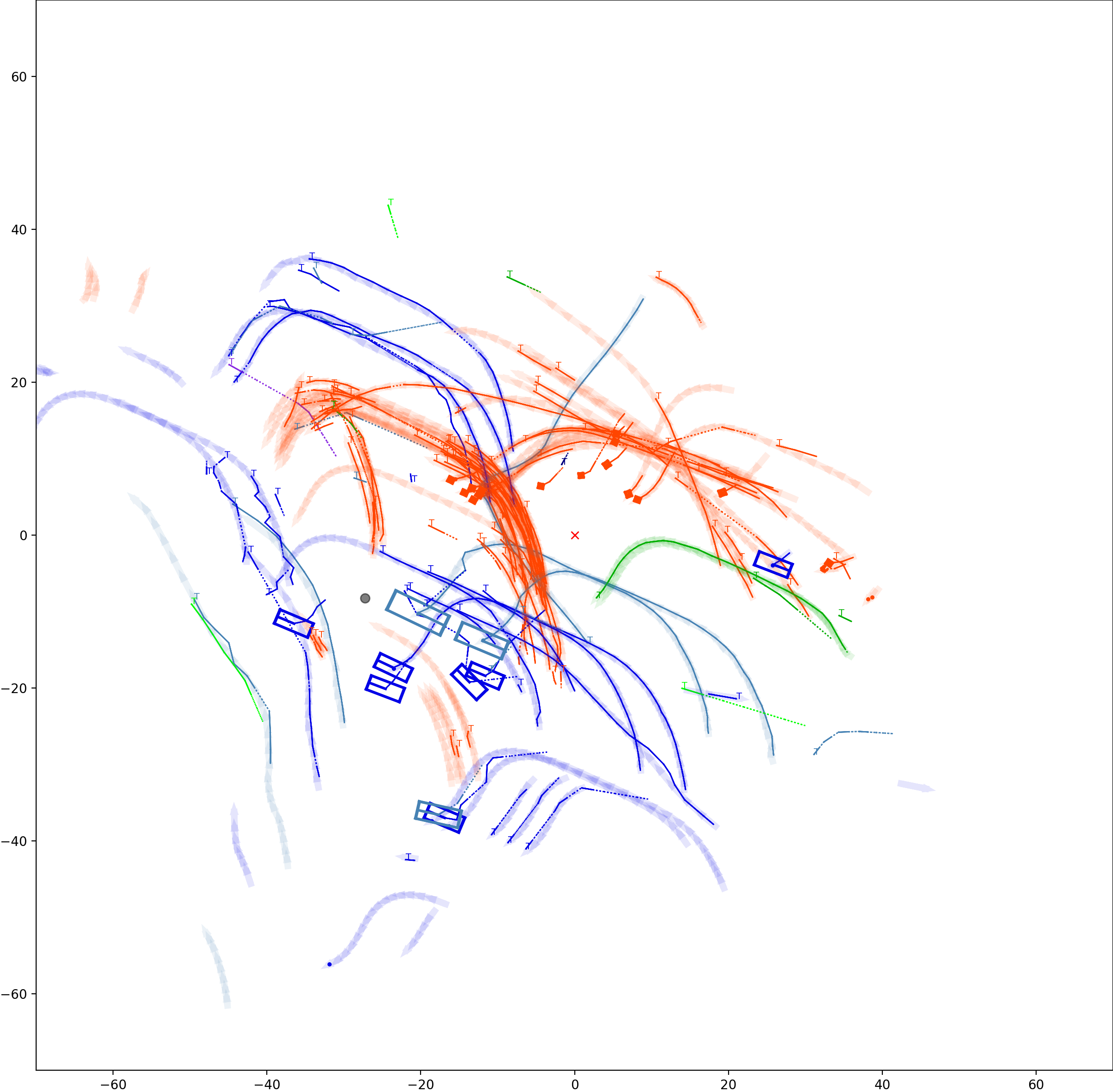
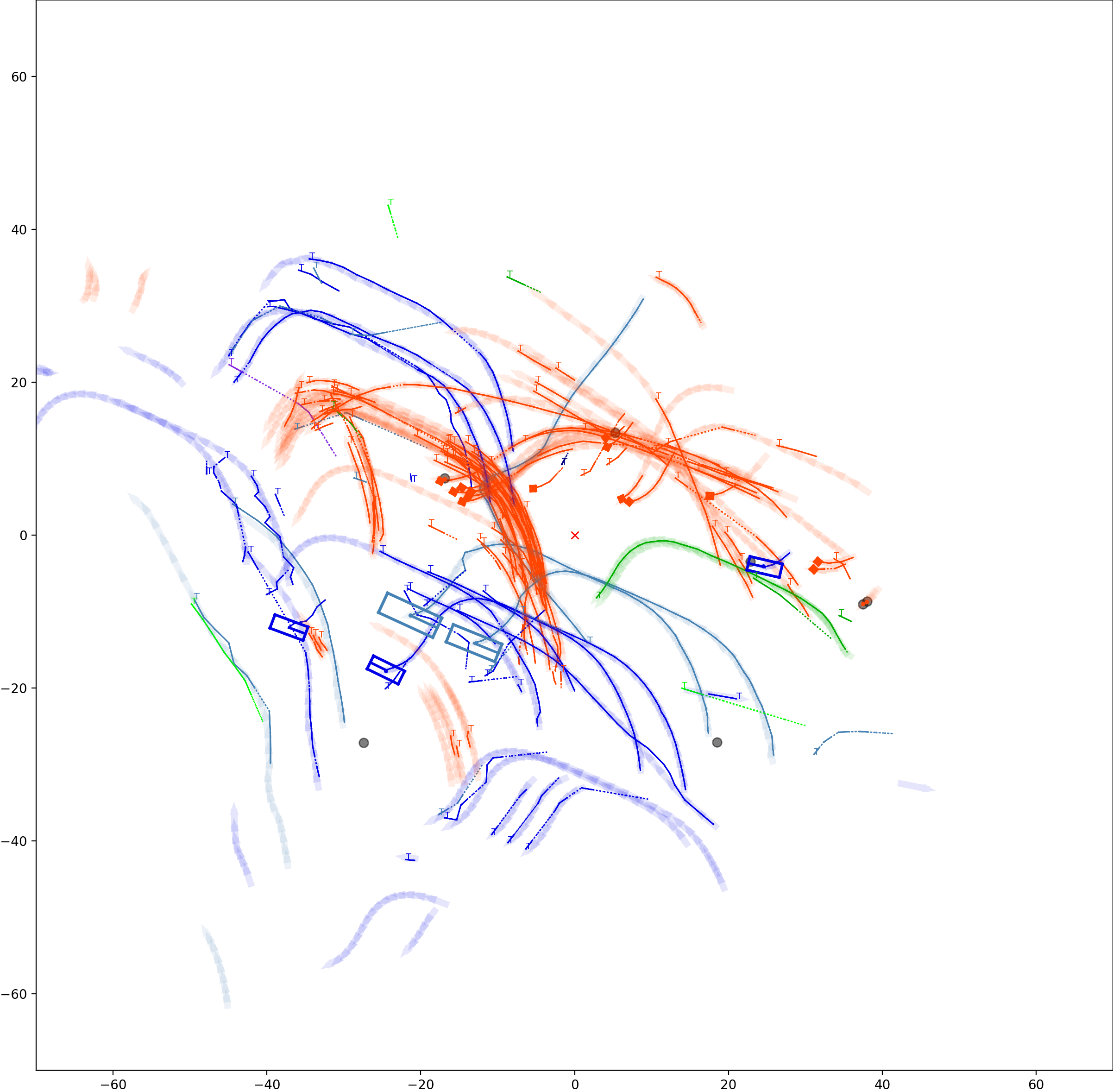
The red cross in the centre represent the position of the ego car. More comprehensive analysis can be found here. Solid coloured boxes represent detection of various categories. The line in the middle of the box represent orientation of the detection. Dashed-line colored boxes represent missed detection in this frame. The transparent lines represents ground truth. The solid lines represent trajectories. The dashed lines in the middle of a solid line represent missed detection in that trajectory.The black dots represent clutter. Letter T indicate that the track has terminated.
Research directions
People are indeed exploring the use of graph neural networks, transformers, language models, and other machine learning techniques for multi-object tracking. At its core, statistical signal processing resembles actuarial science, fundamentally relying on the arguments constructed around statistical models. In my view, the ability to distill problems into models and analyze their properties is a more valuable skill.
Another area of research is extended target tracking. This approach challenges the conventional assumption that each target produces a single detection point, proposing a more realistic scenario in which each target generates an unknown number of detection points. This assumption significantly complicates the statistical modeling.
The concept of 'track before detection' represents another promising research avenue. This approach's statistical modeling extends beyond spatial aspects to include temporal factors, differentiating detection points over time from clutter.
Active information acquisition is another area worth exploring. Tactically designed information acquisition strategies can help overcome physical limitations.
Integrated Sensing and Communication (ISAC) represents a research direction that is attracting significant interest. This context presents numerous open research questions, including those pertaining to the Markov channel capacity and synchronization.
Literature
Durrant-Whyte, H., and T. Bailey. “Simultaneous Localization and Mapping: Part I.” IEEE Robotics & Automation Magazine 13, no. 2 (June 2006): 99–110. https://doi.org/10.1109/MRA.2006.1638022.
Ge, Yu, Ossi Kaltiokallio, Hyowon Kim, Fan Jiang, Jukka Talvitie, Mikko Valkama, Lennart Svensson, Sunwoo Kim, and Henk Wymeersch. “A Computationally Efficient EK-PMBM Filter for Bistatic mmWave Radio SLAM.” IEEE Journal on Selected Areas in Communications 40, no. 7 (July 2022): 2179–92. https://doi.org/10.1109/JSAC.2022.3155504.
Kropfreiter, Thomas, Florian Meyer, David F. Crouse, Stefano Coraluppi, Franz Hlawatsch, and Peter Willett. “Track Coalescence and Repulsion in Multitarget Tracking: An Analysis of MHT, JPDA, and Belief Propagation Methods.” IEEE Open Journal of Signal Processing, 2024, 1–17. https://doi.org/10.1109/OJSP.2024.3451167.
Leitinger, Erik, Paul Meissner, Christoph Rüdisser, Gregor Dumphart, and Klaus Witrisal. “Evaluation of Position-Related Information in Multipath Components for Indoor Positioning.” IEEE Journal on Selected Areas in Communications 33, no. 11 (November 2015): 2313–28. https://doi.org/10.1109/JSAC.2015.2430520.
Leitinger, Erik, and Florian Meyer. “Data Fusion for Multipath-Based SLAM.” In 2020 54th Asilomar Conference on Signals, Systems, and Computers, 934–39, 2020. https://doi.org/10.1109/IEEECONF51394.2020.9443537.
Leitinger, Erik, Florian Meyer, Franz Hlawatsch, Klaus Witrisal, Fredrik Tufvesson, and Moe Z. Win. “A Belief Propagation Algorithm for Multipath-Based SLAM.” IEEE Transactions on Wireless Communications 18, no. 12 (December 2019): 5613–29. https://doi.org/10.1109/TWC.2019.2937781.
Mendrzik, Rico, Florian Meyer, Gerhard Bauch, and Moe Z. Win. “Enabling Situational Awareness in Millimeter Wave Massive MIMO Systems.” IEEE Journal of Selected Topics in Signal Processing 13, no. 5 (September 2019): 1196–1211. https://doi.org/10.1109/JSTSP.2019.2933142.
Venus, Alexander, Erik Leitinger, Stefan Tertinek, Florian Meyer, and Klaus Witrisal. “Graph-Based Simultaneous Localization and Bias Tracking.” IEEE Transactions on Wireless Communications, 2024, 1–1. https://doi.org/10.1109/TWC.2024.3399023.
Yang, Jie, Chao-Kai Wen, and Shi Jin. “Hybrid Active and Passive Sensing for SLAM in Wireless Communication Systems.” IEEE Journal on Selected Areas in Communications 40, no. 7 (July 2022): 2146–63. https://doi.org/10.1109/JSAC.2022.3156630.
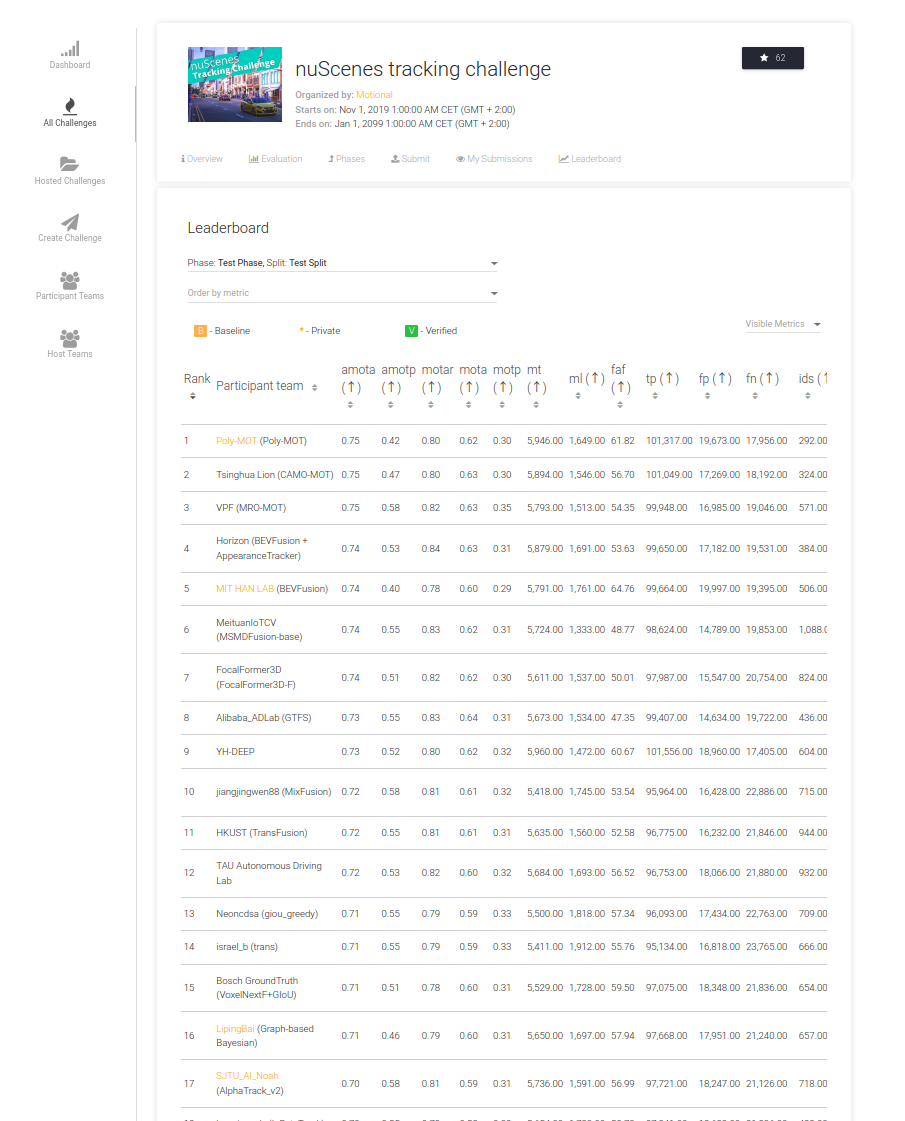
Ranking as of July 2023
The End
|
1. I look forward to the new life in Europe and it is my strongest desire that I can join a great team and make real tangible contributions to the research topic with colleagues. |
|
2. For real data, a lot comes down to implementation. |
|
3. The implicit and unexpected price we have to pay to access any expertise is just sad. |
|
4. As omnipotent as deep learning might be, the abilities to reduce a problem into its most primitive form, to see the problem in its entirety, and to present the problem in a structure that lends itself to clear reasoning are still worthy skills to spend time on. |